投稿者: admin

趣味：写真撮影とデータベース． カメラ：TOYO FIELD, Hasselblad 500C/M, Leica M6． SQL Server 2008 R2, MySQL, Microsoft Access．

偏微分

　x および y に対しての f(x, y) の偏導関数は次式で定義されます．

\displaystyle \frac{\partial f}{\partial x}= \lim\limits_{h \rightarrow 0} \frac{f(x + h, y) - f(x, y)}{h}\\\vspace{0.2 in} \frac{\partial f}{\partial y} = \lim\limits_{k \rightarrow 0} \frac{f(x, y + k) - f(x, y)}{k}

　しばしば h = Δx, k = Δy のように記述します．y を定数とした x に対する f の通常の導関数は単に \partial f/\partial x と記述し，一方 x を定数とした y に対する f の通常の導関数は \partial f/\partial y と記述します．

　高階の導関数もまた同様に定義します．例えば，2 階の通常の導関数は下記のようです．

\displaystyle \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial^2f}{\partial x^2}\\\vspace{0.2 in} \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right) = \frac{\partial^2f}{\partial x\partial y}\\\vspace{0.2 in} \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial^2f}{\partial y\partial x}\\\vspace{0.2 in} \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right) = \frac{\partial^2f}{\partial y^2}

　偏導関数は時々 fx や fy とも記述します．そのような場合 fx(a, b), fy(a, b) は点 (a, b) において評価されるこれらの偏微分です．

　偏導関数はまた fxx, fxy, fyx, fyy とも記述します．f が少なくとも 2 階の連続な偏微分を有するなら 2 階や 3 階微分の結果もまた同様です．

　f(x, y) の全微分は次のように定義します．

\displaystyle df = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy

　ただし h = Δx = dx, k = Δy = dy です．

Functions of two or more variables

The concept of function of one variable can be extended to functions of two or more variables. Thus for example z = f(x, y) defines a function f which assigns to the number pair (x, y) the number z.

It’s familiar for some people with graphing z = f(x, y) in a 3-dimensional xyz coordinate system to obtain a surface. Sometime x and y are called independent variables and z a dependent variable. Occasionally it’s written z = z(x, y) rather than z = f(x, y), using the system z in two different senses. however, no confusion should result.

The ideas of limits and continuity for functions of two or more variables pattern closely those for one variable.

2変数以上の関数

　1 変数関数の概念は 2 変数以上の関数にも拡張可能です．それゆえ例えば z = f(x, y) は 2 つの数 (x, y) を 1 つの数 z に割り付ける関数 f を定義するものです．

　ある人にとっては z = f(x, y) を xyz 座標軸系の 3 次元にグラフ化して面を得ることは馴染み深いでしょう．時には x と y は独立変数と呼ばれ，z は従属変数と呼ばれます．まれに z = f(x, y) ではなく z = z(x, y) と記述されることがあり，z 系は異なる意味で用いられます．しかし混同すべきではありません．

　2 変数以上の関数の極限と連続性の概念は 1 変数のそれに近いです．

Taylor series

The Taylor series for f(x) about x = a is defined as

\displaystyle f(x) = f(a) + f'(a)(x - a) + \frac{f''(a)(x - a)^2}{2!} + \cdots + \frac{f^{n -1}(a)(x - a)^{n-1}}{(n -1)!} + R_n(a)
where \displaystyle R_n = \frac{f^n(x - n)^n}{n!}, x0 between a and x.(b)
is called the reminder and where it is supposed that f(x) has derivatives of order n at least. The case where n = 1 is often called law of the mean or mean-value theorem and can be written as
\displaystyle \frac{f(x) -f(a)}{x - a} = f'(x_0), x0 between a and x (c)

The infinite series corresponding to (a), also called the formal Taylor series for f(x), will converge in some interval if \lim\limits_{n \rightarrow \infty}R_n = 0 in this interval. Some important Taylor series together with their intervals of convergence are as follows.

  1. \displaystyle e^n = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} +\frac{x^4}{4!} + \cdots\ -\infty < x < \infty[/latex]</li> <li>[latex]\displaystyle \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots\ -\infty < x < \infty[/latex]</li> <li>[latex]\displaystyle \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots\ -\infty < x < \infty[/latex]</li> <li>[latex]\displaystyle \ln(1 + x) = x - \frac{x^2}{2!} + \frac{x^3}{3!} - \frac{x^4}{4!} + \cdots\ -1 < x \le 1[/latex]</li> <li>[latex]\displaystyle \tan^{-1}x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots\ -1 \le x \le 1

A series of the form \sum_{n=0}^{\infty}c_n(x - a)^n is often called a power series. Such power series are uniformly convergent in any interval which lies entirely within the interval of convergence.

テーラー級数

　x = a における f(x) のテーラー級数は下記のように定義されます．

\displaystyle f(x) = f(a) + f'(a)(x - a) + \frac{f''(a)(x - a)^2}{2!} + \cdots + \frac{f^{n -1}(a)(x - a)^{n-1}}{(n -1)!} + R_n(a)
ここで \displaystyle R_n = \frac{f^n(x - n)^n}{n!}, x0 は a と x の範囲内(b)
は reminder と呼ばれ， f(x) が最低でも n 次の微分係数を持つと想定します．n = 1 の場合は特に平均の法則または平均値の定理と呼ばれ，次のように記述します．
\displaystyle \frac{f(x) -f(a)}{x - a} = f'(x_0), x0 は a と x の範囲内(c)

　(a) に対応した無限級数は f(x) の正規テーラー級数とも呼ばれ，必ずある区間に収束します．仮に \lim\limits_{n \rightarrow \infty}R_n = 0 がこの区間にあるなら．いくつかの重要なテーラー級数と収束値をその区間とともに示します．

  1. \displaystyle e^n = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} +\frac{x^4}{4!} + \cdots\ -\infty < x < \infty[/latex]</li> <li>[latex]\displaystyle \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots\ -\infty < x < \infty[/latex]</li> <li>[latex]\displaystyle \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots\ -\infty < x < \infty[/latex]</li> <li>[latex]\displaystyle \ln(1 + x) = x - \frac{x^2}{2!} + \frac{x^3}{3!} - \frac{x^4}{4!} + \cdots\ -1 < x \le 1[/latex]</li> <li>[latex]\displaystyle \tan^{-1}x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots\ -1 \le x \le 1

　ある形の級数 \sum_{n=0}^{\infty}c_n(x - a)^n はしばしばべき級数と呼ばれます．そのようなべき級数はどの区間にも一様収束し，それは収束区間内全体にあります．

Uniform convergence

The ideas of previous article can be extended to the case where the un are functions of x denoted by un(x). In such case the sequences or series will converge of diverge according to the particular value of x. The set of values of x for which a sequence or series converges is called the region of convergence, denoted \cal R.

The series u1(x) + u2(x) + … converges to the sum S(x) in a region \cal R if given ε > 0 there exists a number N, which in general depends on both ε and x, such that |S(x) – Sn(x)| < ε whenever n > N where Sn(x) = u1(x) + … + un(x). If you can find N depending only on ε and not on x, the series converges uniformly to S(x) in \cal R. Uniformly convergent series have many important advantages as indicated in the following theorems.

  1. If un(x), n = 1, 2, 3, … are continuous in a ≤ x ≤ b and ∑ un(x) is uniformly convergent to S(x) in a ≤ x ≤ b, then S(x) is continuous in a ≤ x ≤ b.
  2. If ∑u(x) converges uniformly to S(x) in a ≤ x ≤ b and un(x), n = 1, 2, 3, … are integrable in a ≤ x ≤ b, then
    \displaystyle \int^{b}_{a}S(x)dx = \int^{b}_{a}(u_1(x) + u_2(x) + \cdots)dx = \int^{b}_{a}u_1(x)dx + \int^{b}_{a}u_2(x)dx + \cdots
  3. If un(x), n = 1, 2, 3, … are continuous and have continuous derivatives in a ≤ x ≤ b and if ∑un(x) converges to S(x) while ∑u’n(x) is uniformly convergent in a ≤ x ≤ b, then
    \displaystyle S'(x) = \frac{d}{dx}(u_1(x) + u_2(x) + \cdots) = u'_1(x) + u'_2(x) + \cdots
  4. If there is aset of positive constants Mn, n = 1, 2, 3, … such that |un| ≤ Mn in \cal R and ∑Mn converges, then ∑un(x) is uniformly convergent [and also absolutely convergent] in \cal R.

An important test for uniform convergence, often called the Weierstrass M test, is given by the above.

一様収束

　前回の記事で述べた考えは un が x の関数の場合，un(x) と記述するが，に拡張できます．そのような場合，数列または級数が収束するか発散するかは x の特定の値に依存します．数列や級数が収束する x の値の集合は収束領域と呼ばれ，\cal R と表記します．

　級数 u1(x) + u2(x) + … は領域 \cal R 内の S(x) の合計に収束します，もし ε > 0 があってε と x の両者に依存するある数 N があり，|S(x) – Sn(x)| < ε を満たし，常に n > N であって Sn(x) = u1(x) + … + un(x) の場合には．もし ε のみに依存し，x には依存しない N を見つけられるなら，その級数は \cal R 内の S(x) に一様収束します．一様収束級数には次の定理に示すように多くの利点があります．

  1. 仮に un(x), n = 1, 2, 3, … が a ≤ x ≤ b の範囲で連続であり，かつ ∑ un(x) が a ≤ x ≤ b の範囲で S(x) に一様収束するなら S(x) は a ≤ x ≤ b の範囲で連続である．
  2. 仮に ∑u(x) が S(x) に a ≤ x ≤ b の範囲で一様収束し，かつ un(x), n = 1, 2, 3, … が a ≤ x ≤ b の範囲で積分可能である場合は以下が成り立つ．
    \displaystyle \int^{b}_{a}S(x)dx = \int^{b}_{a}(u_1(x) + u_2(x) + \cdots)dx = \int^{b}_{a}u_1(x)dx + \int^{b}_{a}u_2(x)dx + \cdots
  3. 仮に un(x), n = 1, 2, 3, … が連続でかつ a ≤ x ≤ b の範囲で連続して微分可能であり，さらに ∑un(x) が S(x) に収束し，∑u’n(x) が a ≤ x ≤ b の範囲で一様収束するなら以下が成り立つ．
    \displaystyle S'(x) = \frac{d}{dx}(u_1(x) + u_2(x) + \cdots) = u'_1(x) + u'_2(x) + \cdots
  4. 正の定数 Mn が存在し n = 1, 2, 3, … で \cal R 領域内の Mn において |un| ≤ Mn であり，かつ ∑Mn が収束する場合，故に ∑un(x) は \cal R に一様収束する．

　一様収束の重要な判定法があり，しばしば Weierstrass M test と呼ばれますが，上記に示したとおりです．

Sequences and series

A sequence, indicated by u1, u2, …or brief by \langle u_n \rangle, is a function defined on the set of natural numbers. The sequence is said to have the limit l or to converge to l, if given any ε > 0 there exists a number N > 0 such that |un – l| < ε for all n > N, and in such case it is described \lim\limits_{n \rightarrow \infty} u_n =l. If the sequence does not converge, it’s called that it diverges.

Consider the sequence u1, u1 + u2, u1 + u2 + u3, … or S1, S2, S3, … where Sn = u1 + u2 + … + un. It’s called \langle S_n \rangle the sequence of partial sums of the sequence \langle u_n \rangle. The symbol

\displaystyle u_1 + u_2 + u_3 + \cdots or \displaystyle \sum_{n=1}^{\infty}u_n or briefly \displaystyle \sum u_n

is defined as synonymous with \langle S_n \rangle and is called an infinite series. This series will converge or diverge according as \langle S_n \rangle converges or diverges. If it converges to S it’s called S as the sum of the series.

The following are some important theorems concerning infinite series.

  1. The series \displaystyle \sum_{n=1}^{\infty}\frac{1}{n^p} converges if p > 1 and diverges if p ≤ 1.
  2. If ∑|un| converges and |vn| ≤ |un|, then ∑|vn| converges.
  3. If ∑|un| converges, then ∑un converges.
  4. If ∑|un| diverges and vn ≥ |un|, then ∑vn diverges.
  5. The series ∑|un|, where |un| = f(n) ≥ 0, converges or diverges according as \displaystyle \int_{1}^{\infty}f(x)dx = \lim\limits_{M \rightarrow \infty}\int_{1}^{M}f(x)dx exists or does not exist. This theorem is often called the integral test.
  6. The series ∑|un| diverges if \displaystyle \lim\limits_{n \rightarrow \infty}|u_n| \neq 0. However, if \displaystyle \lim\limits_{n \rightarrow \infty}|u_n| = 0 the series may or may not converge.
  7. Suppose that \displaystyle \lim\limits_{n \rightarrow \infty}\left|\frac{u_{n+1}}{n_n}\right| = r. Then the series ∑un converges (absolutely) if r < 1 and diverges if r > 1. If r = 1, no conclusion can be drawn. This theorem is often referred to as the ratio test.

数列と級数

　数列は自然数の集合に基いて定義される関数であり，次のように示されます．u1, u2, … 略記すると \langle u_n \rangle となります．任意の ε > 0 があり，ある数 N > 0 が存在し，|un – l| < ε が全ての n > N について成り立つ時，この数列は極限値 l を持つ，または l に収束するといいます．そのような場合には \lim\limits_{n \rightarrow \infty} u_n =l のように記述します．数列が収束しない場合は発散するといいます．

　次のような数列を考えてみます． u1, u1 + u2, u1 + u2 + u3, … または S1, S2, S3, … ただし Sn = u1 + u2 + … + un．これを \langle S_n \rangle と記述し，数列 \langle u_n \rangle の部分和の数列と呼びます．その記号は

\displaystyle u_1 + u_2 + u_3 + \cdots または \displaystyle \sum_{n=1}^{\infty}u_n または略記して \displaystyle \sum u_n

のように定義し，\langle S_n \rangle と同義であり無限級数と呼びます．この級数が収束するか発散するかは \langle S_n \rangle が収束するか発散するかに依存します．S に収束するなら S は数列の合計と呼びます．

　以下は無限級数についてのいくつかの重要な定理です．

  1. 級数 \displaystyle \sum_{n=1}^{\infty}\frac{1}{n^p} は p > 1 なら収束し， p ≤ 1 なら発散する．
  2. ∑|un| が収束しかつ |vn| ≤ |un| なら ∑|vn| は収束する．
  3. ∑|un| が収束するなら ∑un は収束する．
  4. ∑|un| が発散しかつ vn ≥ |un| なら ∑vn は発散する．
  5. 級数 ∑|un| ただし |un| = f(n) ≥ 0 が収束するか発散するかは \displaystyle \int_{1}^{\infty}f(x)dx = \lim\limits_{M \rightarrow \infty}\int_{1}^{M}f(x)dx が存在するかしないかに依存する．この定理はしばしば積分判定法と呼ばれる．
  6. 級数 ∑|un| は \displaystyle \lim\limits_{n \rightarrow \infty}|u_n| \neq 0 なら発散する．しかしながら，仮に \displaystyle \lim\limits_{n \rightarrow \infty}|u_n| = 0 の場合，級数が収束するか発散するかは分からない．
  7. 次のように仮定してみる．\displaystyle \lim\limits_{n \rightarrow \infty}\left|\frac{u_{n+1}}{n_n}\right| = r. すると級数 ∑un converges (absolutely) は r < 1 なら収束し， r > 1 なら発散する．r = 1 の場合結論は一定ではない．この定理はしばしば比判定法として引用される．

Special types of functions

Polynomials

Polynomial is formula as below;

\displaystyle f(x) = a_0x^n + a_1x^{n-1} + a_2x^{n-2} + \cdots + a_n

If a_0 \neq 0, n is called as degree of polynomials.

\displaystyle (a + x)^n = a^n + \left(\frac{n}{1}\right)a^{n -1}x + \left(\frac{n}{2}\right)a^{n -2}x^2 + \cdots + x^n

where the binomial coefficients are given by

\displaystyle \left(\frac{n}{k}\right) = \frac{n!}{k!(n - k)!}
and where factorial n, i.e. n! = n(n -1)(n-2)…1 while 0! = 1 by definition.

Exponential function

\displaystyle f(x) = a^x

An important special case occurs where a = e = 2.718…

Exponential law

  1. \displaystyle a^{m + n} = a^m \cdot a^n
  2. \displaystyle a^{m - n} = \frac{a^m}{a^n},\ a \neq 0
  3. \displaystyle (a^m)^n = a^{mn}

Logarithmic function

\displaystyle f(x) = \log_a x

These functions are inverse of the exponential functions, i.e. if ax = y then x = logay where a is called the base of the logarithm. If a = e, which is often called the natural base of logarithm, it’s described loge by ln x, called the natural logarithm of x.

Logarithmic law

  1. \displaystyle \ln(mn) = \ln(m) + \ln(n)
  2. \displaystyle \ln\frac{m}{n} = \ln(m) - \ln(n)
  3. \displaystyle \ln{m^p} = p\ln{m}

特殊な関数

多項式

多項式は下記のように表現します．

\displaystyle f(x) = a_0x^n + a_1x^{n-1} + a_2x^{n-2} + \cdots + a_n

　a_0 \neq 0 の時， n は多項式の次数といいます．

\displaystyle (a + x)^n = a^n + \left(\frac{n}{1}\right)a^{n -1}x + \left(\frac{n}{2}\right)a^{n -2}x^2 + \cdots + x^n

二項係数は下記のように表現します．

\displaystyle \left(\frac{n}{k}\right) = \frac{n!}{k!(n - k)!}

n の階乗は n! = n(n -1)(n-2)…1 であり，定義上 0! = 1 となります．

指数関数

\displaystyle f(x) = a^x

　a = e = 2.718… の時，特殊な例が発生します．

指数法則

  1. \displaystyle a^{m + n} = a^m \cdot a^n
  2. \displaystyle a^{m - n} = \frac{a^m}{a^n},\ a \neq 0
  3. \displaystyle (a^m)^n = a^{mn}

対数関数

\displaystyle f(x) = \log_a x

対数関数は指数関数の逆関数です．仮に ax = y である時，逆関数は x = logay であり a は対数の底と呼びます．a = e の時，それを自然対数の底と呼び，x の自然対数 logex のことを ln x と表現します．

対数法則

  1. \displaystyle \ln(mn) = \ln(m) + \ln(n)
  2. \displaystyle \ln\frac{m}{n} = \ln(m) - \ln(n)
  3. \displaystyle \ln{m^p} = p\ln{m}

Integrals

Integrals

If dy/dx = f(x), then it’s called that y an indefinite integral of f(x) and denoted as

\displaystyle \int f(x)dx

If f(x) = \frac{d}{dx}F(x), then

\displaystyle \int_a^b f(x)dx = F(b) - F(a)

Integral formulas

In the following u, v represent functions of x while a, b, c, p represent constants.

\displaystyle \int (u \pm v)dx = \int u dx \pm \int v dx\\\vspace{0.2 in} \int cu dx = c\int u dx \\\vspace{0.2 in} \int u\left(\frac{dv}{dx}\right) = uv - \int v \left(\frac{du}{dx}\right)dx \\\vspace{0.2 in} \int u dv = uv - \int v du

This is called integration by parts.

\displaystyle \int F(u(x))dx = \int F(w)\frac{dw}{dw/dx}

where w = u(x) and w’ = dw/dx expressed as a function of w. This is called integration by substitution or tranformation.

\displaystyle \int u^p du = \frac{u^{p+1}}{p+1},\ p \neq -1\\\vspace{0.2 in} \int u^{-1}du = \int \frac{du}{u} = \ln u\\\vspace{0.2 in} \int a^u du = \frac{a^u}{\ln a},\ a \neq 0,\ 1\\\vspace{0.2 in} \int e^u du = e^u

\displaystyle \int \sin u\ du = -\cos{u}\\\vspace{0.2 in} \int \cos u\ du = \sin{u}\\\vspace{0.2 in} \int \tan u\ du = -\ln \cos{u}\\\vspace{0.2 in} \int e^{au}\sin{bu}\ du = \frac{e^{au}(a\ \sin{bu}- b\ \cos{bu})}{a^2 + b^2}\\\vspace{0.2 in} \int e^{au}\cos{bu}\ du = \frac{e^{au}(a\ \cos{bu}+ b\ \sin{bu})}{a^2 + b^2}\\\vspace{0.2 in} \int \frac{du}{\sqrt{a^2 - u^2}} = \sin^{-1}\frac{u}{a}\\\vspace{0.2 in} \int \frac{du}{u^2 + a^2} = \frac{1}{a}\tan^{-1}\frac{u}{a}\\\vspace{0.2 in} \int \frac{du}{\sqrt{u^2 - a^2}} = \ln(u + \sqrt{u^2 - a^2})\\\vspace{0.2 in} \int \frac{du}{\sqrt{u^2 + a^2}} = \ln(u + \sqrt{u^2 + a^2})

積分

積分

　ある関数について dy/dx = f(x) である時，y は次のように表現されます．

\displaystyle \int f(x)dx

　f(x) = \frac{d}{dx}F(x) の時，積分は以下のように定義されます．

\displaystyle \int_a^b f(x)dx = F(b) - F(a)

積分公式

　関数 u, v および定数 a, b, c, p について下記が成り立ちます．

\displaystyle \int (u \pm v)dx = \int u dx \pm \int v dx\\\vspace{0.2 in} \int cu dx = c\int u dx \\\vspace{0.2 in} \int u\left(\frac{dv}{dx}\right) = uv - \int v \left(\frac{du}{dx}\right)dx \\\vspace{0.2 in} \int u dv = uv - \int v du \\\vspace{0.2 in} \int F(u(x))dx = \int F(w)\frac{dw}{dw/dx},\ w = u(x) \displaystyle \int u^p du = \frac{u^{p+1}}{p+1},\ p \neq -1\\\vspace{0.2 in} \int u^{-1}du = \int \frac{du}{u} = \ln u\\\vspace{0.2 in} \int a^u du = \frac{a^u}{\ln a},\ a \neq 0,\ 1\\\vspace{0.2 in} \int e^u du = e^u \displaystyle \int \sin u\ du = -\cos{u}\\\vspace{0.2 in} \int \cos u\ du = \sin{u}\\\vspace{0.2 in} \int \tan u\ du = -\ln \cos{u}\\\vspace{0.2 in} \int e^{au}\sin{bu}\ du = \frac{e^{au}(a\ \sin{bu}- b\ \cos{bu})}{a^2 + b^2}\\\vspace{0.2 in} \int e^{au}\cos{bu}\ du = \frac{e^{au}(a\ \cos{bu}+ b\ \sin{bu})}{a^2 + b^2}\\\vspace{0.2 in} \int \frac{du}{\sqrt{a^2 - u^2}} = \sin^{-1}\frac{u}{a}\\\vspace{0.2 in} \int \frac{du}{u^2 + a^2} = \frac{1}{a}\tan^{-1}\frac{u}{a}\\\vspace{0.2 in} \int \frac{du}{\sqrt{u^2 - a^2}} = \ln(u + \sqrt{u^2 - a^2})\\\vspace{0.2 in} \int \frac{du}{\sqrt{u^2 + a^2}} = \ln(u + \sqrt{u^2 + a^2})

Derivatives

Derivatives

The derivative of y = f(x) at a point x is defined as

\displaystyle f'(x) = \lim\limits_{h \rightarrow 0}\frac{f(x+h) - f(x)}{h} = \lim\limits_{\Delta x \rightarrow 0}\frac{\Delta y}{\Delta x} = \frac{dy}{dx}

where h = Δx, Δy = f(x + h) – f(x) = f(x + Δx) – f(x) provided the limit exists.

Differentiation formulas

In the following u, v represent function of x while a, c, p represent constants. It’s assumed that the derivatives of u and v exist, i.e. u and v are differentiable.

\displaystyle \frac{d}{dx}(u \pm v) = \frac{du}{dx} \pm \frac{dv}{dx}\\\vspace{0.2 in} \frac{d}{dx}(cu) = c\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}(uv) = u\frac{dv}{dx} + v\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}\left(\frac{u}{v}\right) = \frac{v(du/dx) - u(dv/dx)}{v^2}\\\vspace{0.2 in} \frac{d}{dx}u^p = pu^{p-1}\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}(a^u) = a^u\ln{a}\\\vspace{0.2 in} \frac{d}{dx}e^u = e^u\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}\ln{u} = \frac{1}{u}\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}\sin{u} = \cos{u}\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}\cos{u} = -\sin{u}\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}\tan{u} = \sec^2{u}\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}\sin^{-1}u = \frac{1}{\sqrt{1 - u^2}}\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}\cos^{-1}u = \frac{-1}{\sqrt{1 - u^2}}\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}\tan^{-1}u = \frac{1}{\sqrt{1 + u^2}}\frac{du}{dx}

In the special case where u = x, the above formulas are simplified since in such case du/dx = 1.

Rules of algebra

If a, b, c are any real numbers, the following rules of algebra hold.

  1. Commutative law for addition
  2. Associative law for addition
  3. Commutative law for multiplication
  4. Associative law for multiplication
  5. Distributive law

Commutative law for addition

\displaystyle a + b = b + a

Associative law for addition

\displaystyle a + (b + c) = (a + b) + c

Commutative law for multiplication

\displaystyle ab = ba

Associative law for multiplication

\displaystyle a(bc) = (ab)c

Distributive law

\displaystyle a(b + c) = ab + ac

How to get partial correlation matrix to validate multicollinearity in multivariate analysis with EXCEL?

In order to validate multicollinearity in multivariate analysis, you could investigate signs of partial correlation matrix. You could calculate partial correlation coefficient, rij rest, when you would be given covariates without xi and xj and it’s assumed that R = (rij) as correlation matrix and R-1 = (rij) as inverse matrix, respectively.

\displaystyle r_{ij\cdot rest} = - \frac{r^{ij}}{\sqrt{r^{ii}r^{jj}}}

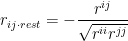
Reverse the sign of the elements divided by square of products of the diagonal elements, they are partial correlation coefficients. The set of partial correlation coefficients is partial correlation matrix.

\displaystyle R=\left( \begin{array} {cccccc} 1 \\ r_{21} & 1 \\ \vdots & \ddots & 1 \\ r_{i1} & \ldots & r_{ij} & 1 \\ \vdots & & \vdots & \ddots & 1 \\ r_{n1} & \ldots & r_{nj} & \ldots & r_{nn-1} & 1 \\ \end{array} \right) \displaystyle R^{-1}=\left( \begin{array} {cccccc} r^{11} \\ r^{21} & \ddots \\ \vdots & \ddots & r^{jj} \\ r^{i1} & \ldots & r^{ij} & r^{ii} \\ \vdots & & \vdots & \ddots & \ddots \\ r^{n1} & \ldots & r^{nj} & \ldots & r^{nn-1} & r^{nn} \\ \end{array} \right)

When the signs didn’t match between correlation matrix and partial correlation matrix, it suggests multicollinearity. When there was linear relationship between covariates, inverse matrix of correlation matrix could not be obtained.

You could get partial correlation matrix as below. It’s assumed that you have already get correlation matrix.

  1. Get inverse matrix of correlation matrix
  2. Divide each elements of inverse matrix by square of product of diagonal elements and reverse the sign
　 A B C
1 1.000 0.800 0.300
2 0.800 1.000 -0.700
3 0.300 -0.700 1.000

1. Get inverse matrix of correlation matrix

Excel has worksheet function to get inverse matrix. You need to press the Control key, Shift key and Enter key at the same time when you confirm the argument as MINVERSE function.

{=MINVERS($A$1:$C$3)}

　 A B C
5 -0.197 1.817 1.547
6 1.817 -1.637 -1.691
7 1.547 -1.691 -0.647

2. Divide each elements of inverse matrix by square of product of diagonal elements and reverse the sign

You would have to use INDEX function, ROW function and COLUMN function. Paste following formula to the corresponding cells. The number subtracted from the return of ROW function (and COLUMN function) would change depending on the situation.

=-INDEX($A$5:$C$7, ROW()-8,COLUMN())/SQRT(INDEX($A$5:$C$7, ROW()-8, ROW()-8)*INDEX($A$5:$C$7, COLUMN(),COLUMN()))

　 A B C
9 1.000 -1.483 -2.007
10 -1.483 1.000 1.642
11 -2.007 1.642 1.000

多変量解析の多重共線性を調べるために相関行列から偏相関行列をExcelで求める方法

　多変量解析において変数間の多重共線性を調べる方法の一つに偏相関行列があります．相関行列を R = (rij) とし，その逆行列を R-1 = (rij) とすると，xi と xj 以外のすべての変数を与えた時の xi と xj の偏相関係数 rij rest は下式で表現できます．

\displaystyle r_{ij\cdot rest} = - \frac{r^{ij}}{\sqrt{r^{ii}r^{jj}}}

　逆行列の対応する要素を2つの対角要素の積の平方根で割って基準化し，符号を反転します．この偏相関係数を全ての変数の対について行列の形にまとめたものを偏相関行列と言います．

\displaystyle R=\left( \begin{array} {cccccc} 1 \\ r_{21} & 1 \\ \vdots & \ddots & 1 \\ r_{i1} & \ldots & r_{ij} & 1 \\ \vdots & & \vdots & \ddots & 1 \\ r_{n1} & \ldots & r_{nj} & \ldots & r_{nn-1} & 1 \\ \end{array} \right) \displaystyle R^{-1}=\left( \begin{array} {cccccc} r^{11} \\ r^{21} & \ddots \\ \vdots & \ddots & r^{jj} \\ r^{i1} & \ldots & r^{ij} & r^{ii} \\ \vdots & & \vdots & \ddots & \ddots \\ r^{n1} & \ldots & r^{nj} & \ldots & r^{nn-1} & r^{nn} \\ \end{array} \right)

　相関行列と偏相関行列の符号が一致しない場合は多重共線性の可能性があります．また，変数間に線形の関係がある場合は相関行列の逆行列が求まらないこともあります．

　Excelで偏相関行列を求める方法は下記の通りです．既に相関行列は求まっているものとします．

  1. 相関行列の逆行列を求める
  2. 逆行列の各要素を2つの対角要素の積の平方根で割り，符号を逆転する

 

　 A B C
1 1.000 0.800 0.300
2 0.800 1.000 -0.700
3 0.300 -0.700 1.000

1. 相関行列の逆行列を求める

　逆行列を求めるワークシート関数は Excel に標準装備されています．MINVERS 関数を用いる時の注意点として，関数の引数として相関行列を指定し，確定する際に Control キーと Shift キーと Enter キーを同時に押下する必要があります．

{=MINVERS($A$1:$C$3)}

　 A B C
5 -0.197 1.817 1.547
6 1.817 -1.637 -1.691
7 1.547 -1.691 -0.647

2. 逆行列の各要素を2つの対角要素の積の平方根で割り，符号を逆転する

　求まった逆行列の各要素から2つの対角要素のアドレスを求めるには少々工夫が必要です．INDEX 関数と ROW 関数および COLUMN 関数を組み合わせます．下式を該当セルにペーストします．ROW 関数（および COLUMN 関数）から差し引いている数値は INDEX 関数の第 1 引数の 2 次元配列の行番号（と列番号）を指定するものですので，状況によって数値は変化します．各自で対応して下さい．

=-INDEX($A$5:$C$7, ROW()-8,COLUMN())/SQRT(INDEX($A$5:$C$7, ROW()-8, ROW()-8)*INDEX($A$5:$C$7, COLUMN(),COLUMN()))

　 A B C
9 1.000 -1.483 -2.007
10 -1.483 1.000 1.642
11 -2.007 1.642 1.000

How to calculate variance inflation factor (VIF) in multivariate analysis, that influences multicollinearity?

Multicollinearity, which occurs when there is strong correlation between the variables, cause serious problems in multivariate analysis. One of the indicators of multicollinearity is variance inflation factor (VIF). It’s threshold is 10. When VIF would be 10 or larger, the impact of multicollinearity could be strong, therefore the variable should be removed.

  • Regression equation changes significantly when you add or remove a small number of data
  • Regression equation changes significantly when you applied to different data set
  • Sign of the regression coefficient is opposite to the common sense of the field
  • Although the contribution rate of regression equation is high and the model fitting is good, individual regression coefficients is not significant
  • Regression equation can not be obtained

When you encountered the phenomenon above list, you should consider multicollinearity. It’s assumed that one variable is objective and other variables are explanatory variables. You could calculate multiple correlation coefficient (R-square) by linear regression analysis with such spreadsheet software as EXCEL, and calculate VIF as following formula.

\displaystyle VIF = \frac{1}{1 - R^2}

VIF measures the impact of multicollinearity among the X’s in a regression model on the precision of estimation. It expresses the degree to which multicollinearity amongst the predictors degrades the precision of an estimate. VIF is a statistic used to measure possible multicollinearity amongst the predictor or explanatory variables. VIF is computed as (1/(1-R2)) for each of the k – 1 independent variable equations. For example, given 4 independent predictor variables, the independent regression equations are formed by using each k-1 independent variable as the dependent variable:
X1 = X2 X3 X4
X2 = X1 X3 X4
X3 = X1 X2 X4
Each independent variable model will return an R2 value and VIF value. The term to exclude in the model is then based on the value of VIF. If Xj is highly correlated with the remaining predictors, its variance inflation factor will be very large. A general rule is that the VIF should not exceed 10 (Belsley, Kuh, & Welsch, 1980). When Xj is orthogonal to the remaining predictors, its variance inflation factor will be 1.

Clearly the shortcomings just mentioned in regard to the use of R as a diagnostic measure for collinearity would seem also to limit the usefulness of R-1 , and this is the case. The prevalence of this measure, however, justifies its separate treatment. Recalling that we are currently assuming the X data to be centered and scaled for unit length, we are considering R-1 = (XTX)-1. The diagonal elements of R-1, the rii, are often called the variance inflation factors, VIFi, [Chatterjee and Price (1077)], and their diagnostic value follows from the relation
\displaystyle VIF_i = \frac{1}{1-R^2_i}
where Ri2 is the multiple correlation coefficient of Xi regressed on the remaining explanatory variables. Clearly a high VIF indicates an Ri2 near unity, and hence points to collinearity. This measure is therefore of some use as an overall indication of collinearity. Its weakness, like those of R, lie in its inability to distinguish among several coexisting near dependencies and in the lack of a meaningful boundary to distinguish between values of VIF that can be considered high and those that can be considered low. [Belsley]

References:
Cecil Robinson and Randall E. Schumacker: Interaction Effects: Centering, Variance Inflation Factor, and Interpretation Issues. Multiple Linear Regression Viewpoints, 2009, Vol. 35(1)
Belsley, D. A.: Demeaning conditioning diagnostics through centering: The American Statistics 1984; 38: 73 – 82