Any first order differential equation can be put into the form
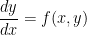
or
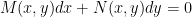
and the general solution of such an equation contains one arbitrary constant. Many special devices are available for finding general solutions of various types of first order differential equations. In the following list some of types are given.
- Separation of variables
- Exact equation
- Integrating factor
- Linear equation
- Homogeneous equation
- Bernoulli’s equation
- Equation solvable for y
- Clairaut’s equation
- Miscellaneous equations
1. Separation of variables
If differential equation is given as below,
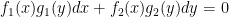
divide by 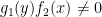 and integrate to obtain general solution
and integrate to obtain general solution

2. Exact equation
If differential equation is given as below,
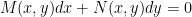
where 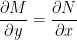
The equation can be written as

where dU is an exact differential. Thus the solution is 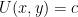 or equivalently
or equivalently

where δx indicates that the integration is to be performed with respect to x keeping y constant.
3. Integrating factor
If differential equation is given as below,
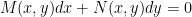
where

The equation can be written as an exact differential equation

where μ is an appropriate integrating factor.
The following combination are often useful in finding integration factors.
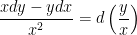

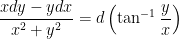
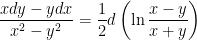
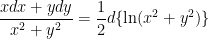
4. Linear equation
If differential equation is given as below,
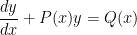
An integrating factor is given by

and the equation can then be written
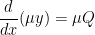
with solution
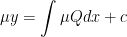
or

5. Homogeneous equation
If differential equation is given as below,
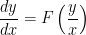
Let 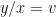 or
or 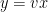 , and the equation becomes
, and the equation becomes
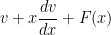
or

which is of Type 1 and has the solution
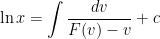
where 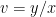 . If
. If 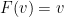 , the solution is
, the solution is 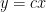 .
.
6. Bernoulli’s equation
If differential equation is given as below,

Letting  , the equation reduces to Type 4 with solution
, the equation reduces to Type 4 with solution

If n = 0, the equation is of Type 4. If n = 1, it is of Type 1.
7. Equation solvable for y
If differential equation is given as below,

where

Differentiate both sides of the equation with respect to x to obtain

or

Then solve this last equation to obtain  . The required solution is obtained by eliminating p between
. The required solution is obtained by eliminating p between  and
and  .
.
An analogous method exists if the equation is solvable for x.
8. Clairaut’s equation
If differential equation is given as below,
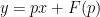
where

The equation is of Type 7 and has solution
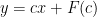
The equation will also have a singular solution in general.
9. Miscellaneous equations
If differential equation is given as below,

(a)Letting 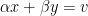 , the equation reduces Type 1.
, the equation reduces Type 1.
(b)Let  and choose constants h and k so that the equation reduces to Type 5. This is possible if and only if
and choose constants h and k so that the equation reduces to Type 5. This is possible if and only if 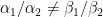 . If
. If  , the equation reduces to Type 9(a).
, the equation reduces to Type 9(a).
等を見出すことができます.十分に小さな
を選ぶことで良い近似が得られます.
が得られます.そしてその解は,その級数が収束することを前提に,次のテイラー級数で得られます.
が得られます.
を前提として (5) から次の新しい近似式が得られます.
を得ます.この一連の近似式の極限は,もし存在するなら,求められる解です.しかしながら数回の手順を行うことで良い近似が得られます.








