カテゴリー: Mathematics

In evaluating a multiple integral over a region , it is often convenient to use coordinates other than rectangular, such as the curvilinear coordinates considered in Chapter 5.

If we let be curvilinear coordinates of points in a plane, there will be a set of transformation equations mapping points of the xy plane into points of the uv plane. In such case the region of the xy plane is mapped into a region of the uv plane. We then have

where and

is the Jacobian of x and y with respect to u and v.

Similarly if are curvilinear coordinates in three dimensions, there will be a set of transformation equations , , and we can write

where and

is the Jacobian of x, y and z with respect to u, v and w.

The results (9) and (11) correspond to change of variables for double and triple integrals.

Generalizations to higher dimensions are easily made.

　領域 上の多重積分を評価するにあたり，直交系以外の座標，例えば第5章で考慮したような曲線座標をしばしば便利に用いることがあります．

　仮に をある平面上の点の曲線座標とすると，xy 平面の点 を uv 平面の点 にマッピングする変換式のセット が得られるはずです．その場合 xy 平面の領域 は uv 平面の領域 にマッピングされます．ここで次の式を得ます．

ここで および

は u および v についての x および y の ヤコビアン です．

　同様に を3次元における曲線座標とするなら , , という変数変換式セットが得られ，下記のように記述します．

ここで および

上記は u, v and w に関する x, y および z の ヤコビアン です．

　その結果 (9) および (11) は二重積分及び三重積分の変数変換に対応します．

　より高次への一般化も容易に可能です．

The above results are easily generalized to closed regions in three dimensions. For example, consider a function defined in a closed three dimensional region . Subdivided the region into n subregions of volume . Letting be some point in each subregion, we form

where the number n of subdivisions approaches infinity in such a way that the largest linear dimension of each subregion approaches zero. If this limit exists we denote it by

called the triple integral of over . The limit dose exist if is continuous (or piecewise continuous) in .

If we construct a grid consisting of planes parallel to the xy, yz and xz planes, the region is subdivided into subregions which are rectangular parallelepipeds. In such case we can express the triple integral over given by (7) as an iterated integral of the form

(where the innermost integral is to be evaluated first) or the sum of such integrals. The integration can also be performed in any other order to give an equivalent result.

Extensions to higher dimensions are also possible.

　上述の結果は3次元での閉じた領域に容易に拡張できます．例えば，3次元の閉領域 において定義される関数 について考えてみましょう．その領域を体積 で n 個の小領域に細分化します． を各々の小領域内のある点とすると，以下を形成します．

ここで細分化の個数 n は無限大に増大し，各々の小領域の最大線長はゼロに近づきます．仮にこの極限が存在するなら次のように記述します．

これを における の 三重積分 と呼びます． が において連続または区間的に連続ならその極限は存在します．

　xy, yz および xz 平面に平行な平面でグリッドを形成するなら，領域 は直方体の小領域に細分化されます．そのような場合，(7) で与えられる における三重積分を 逐次積分 と表現します．

ここで最内側の積分を最初に評価し，またそのような積分の和として表現します．その積分は同等の結果を与える任意の他の順序で行うことができます．

　より高次への一般化も容易です．

If is such that any lines parallel to the y axis meet the boundary of in at most two points, then we can write the equation of the curves ACB and ADB bounding as and respectively, where and are single-valued and continuous in . In this case we can evaluate the double integral (3) by choosing the regions as rectangles formed by constracting a grid of lines parallel to the x and y axes and as the corresponding areas. Then (3) can be written

where the integral in braces is to be evaluated first (keeping x constant) and finally integrating with respect to x from a to b. The result (4) indicates how a double integral can be evaluated by expressing it in terms of two single integrals called iterated integrals.

If is such that any lines parallel to the x axis meet the boundary of in at most two points, then the equations of curves CAD and CBD can be written and respectively and we find similarly

If the double integral exists, (4) and (5) will in general yield the same value. In writing a double integral, either of the forms (4) or (5), whichever is appropriate, may be used. We call one form an interchange of the order of integration with respect to the other form.

In case is not of the type shown in the above figure, it can generally be subdivided into regions which are of this type. Then the double integral over is found by taking the sum of the double integrals over .

仮に が y 軸に平行なあらゆる線が，せいぜい2点における の境界に接するなら， に接する曲線 ACB および ADB の等式をそれぞれ および と記述できます．ここで および は において単一値で連続です．この場合，二重積分 (3) を評価できます．領域 を x 軸及び y 軸に平行な直線でグリッドを形成し， をそれに対応する面積とする長方形として選択します．ゆえに (3) は次のように記述できます．

ここで（ x を定数として扱い）括弧内の積分を最初に評価し，最後に x について a から b まで積分します．その結果 (4) は二重積分がどう評価されるかを示しています．それを2つの単独の積分という面で表現すると 逐次積分 と呼びます．

仮に において，2点で の境界に接する x 軸に平行ないかなる直線でも曲線 CAD および CBD の式は および と記述でき，同様に以下のことが分かります．

仮に二重積分が存在するなら (4) および (5) からは一般に同じ値が得られる筈です．二重積分を記述する際， (4) または (5) のいずれの形でも適切な方が用いられます．これを他には 積分順序の交換 とも呼びます．

が上図で表現した形でない場合は，この形 に細分化します．ゆえに の二重積分は の二重積分の和として見つかります．

Let be defined in a closed region of the plane. Subdivided into subregions of area . Let be some point of . Form the sum

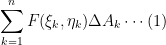
Consider

where the limit is taken so that the number n of subdivisions increases without limit and such that the largest linear dimension of each approaches zero. If this limit exists it is denoted by

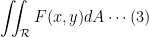
and is called the double integral of F(x, y) over the region .

It can be proved that the limit dose exist if is continuous (or piecewise continuous) in .

を 平面の閉領域 内に定義します． を面積が で 個の小領域 に細分化します． を のある点とします．次のように和を形成します．

以下を考えてみましょう．

ここで極限は細分化された n の数が無限に増大し，またそれぞれの の最大長の次元はゼロに近づいていくものとします．このような極限が存在する時，次のように記述します．

そしてこれを領域 における F(x, y) の 二重積分 と呼びます．

仮に において が連続，または区間的に連続なら極限は存在すると証明できます．

• DOUBLE INTEGRALS
• ITERATED INTEGRALS
• TRIPLE INTEGRALS
• TRANSFORMATIONS OF MULTIPLE INTEGRALS
• LINE INTEGRALS
• VECTOR NOTATION FOR LINE INTEGRALS
• EVALUATION OF LINE INTEGRALS
• PROPERTIES OF LINE INTEGRALS
• SIMPLE CLOSED CURVES. SIMPLY AND MULTIPLY-CONNECTED REGIONS
• GREEN’S THEOREM IN THE PLANE
• CONDITIONS FOR A LINE INTEGRAL TO BE INDEPENDENT OF THE PATH
• SURFACE INTEGRALS
• THE DIVERGENCE THEOREM
• STOKE’S THEOREM

• 二重積分
• 逐次積分
• 三重積分
• 多重積分の変数変換
• 線積分
• 線積分のベクトル表記
• 線積分の評価/li>
• 線積分の属性
• 単純閉曲線．単連結領域および多重連結領域
• 平面におけるグリーンの定理
• 線積分が経路独立であるための条件
• 面積分
• 発散定理
• ストークスの定理

If is an matrix, we can think of it as an operator or transformation acting on a column vector to produce which is another column vector. With this interpretation equation (21) asks for those vectors which are transformed by into constant multiples of themselves [or equivalently into vectors which have the same direction but possibly different magnitude].

If case is an orthogonal matrix, the transformation is a rotation and explains why the absolute value of all the eigenvalues in such case are equal to one, since an ordinary rotation of a vector would not change its magnitude.

The ideas of transformation are very convenient in giving interpretations to many properties of matrices.

仮に が 次行列とすると，列ベクトル に作用して別の列ベクトル を形成する演算子 または 変換 と考えることができます．この解釈によると方程式 (21) はそれらのベクトル に， によりそれら自身の定数倍（または同じ方向を持ち大きさの異なる同等のベクトル）に変換されたのはどちらだろうかという疑問が生じます．

　仮に が直交行列の場合，その変換は 回転 となり，そのような場合になぜ全ての固有値の絶対値が 1 に等しくなるか説明できます．なぜなら通常ベクトルの回転はその大きさを変えないからです．

　この変換の考えは行列の属性への解釈を与える際に非常に便利です．

Theorem 12. The eigenvalues of a Hermitian matrix [or symmetric real matrix] are real. The eigenvalues of a skew-Hermitian matrix [or skew-symmetric real matrix] are zero or pure imaginary. The eigenvalues of a unitary [or real orthogonal matrix] all have absolute value equal to 1.

Theorem 13. The eigenvectors belonging to different eigenvalues of a Hermitian matrix [or symmetric real matrix] are orthogonal.

Theorem 14. [Cayley-Hamilton] A matrix satisfies its own characteristic equation.

Theorem 15. [reduction of matrix to diagonal form] If a non-singular matrix has distinct eigenvalues with corresponding eigenvectors written as columns in the matrix

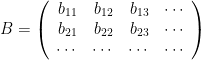
then

i.e. , called the transform of by , is a diagonal matrix containing the eigenvalues of in the main diagonal and zeros elsewhere. We say that has been transformed or reduced to diagonal form.

Theorem 16. [Reduction of quadratic form to canonical form] Let be a symmetric matrix, for example,

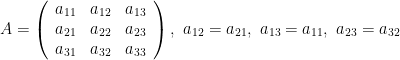
Then if , we obtain the quadratic form

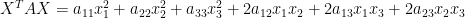
The cross product terms of this quadratic form can be removed by letting where is the column vector with elements and is an orthogonal matrix which diagonalizes . The new quadratic form in with no cross product terms is called the canonical form. A generalization can be made to Hermitian quadratic forms.

定理 12. エルミート行列（または実対称行列）の固有値は実数です．歪エルミート行列（または歪対称実行列）の固有値はゼロまたは純虚数です．ユニタリ行列（または実直交行列）の固有値はすべて絶対値は 1 に等しくなります．

定理 13. エルミート行列（または実対称行列）の異なる固有ベクトルに属する固有ベクトルは直交します．

定理 14. （ケーリー・ハミルトン） ある行列は自身の特性方程式を満たします．

定理 15. （対角形への行列の縮約） ある正則行列 に明確な固有値 があって対応する固有ベクトルが行列の中で列として記述されるなら

すると

すなわち は による の 変換 と呼び， の固有値を主対角線上に持ち，他はすべてゼロの対角行列です． は 変換された または 対角形に縮約された といいます．

定理 16. （二次形式の標準形への縮約） を対称行列とします．例えば

　すると仮に ならば 二次形式 が得られます．

　この二次形式の外積の項は と置くことで除去されますが，ここで は の要素を持つ列ベクトルです．また は直交行列で を直交化したものです． における新しい二次形式には外積の項がなく 標準形 と呼びます．一般化はエルミート二次形式によりなされます．

Let be an matrix and a column vector. The equation

where is a number can be written as

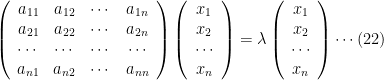
or

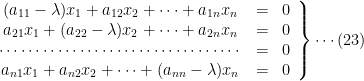
The equation (23) will have non-trivial solution if and only if

which is a polynomial equation of degree n in . The roots of this equation are called eigenvalues or characteristic values of the matrix . Corresponding to each eigenvalue there will be a solution , i.e. a non-trivial solution, which is called an eigenvector or characteristic vector belonging to the eigenvalue. The equation (24) can also be written

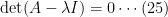
and the equation in is often called the characteristic equation.

　 を 行列とし を列ベクトルとしましょう．以下の方程式について

ここで は数であり以下のように記述できます．

あるいは

　方程式 (23) は以下の場合にのみ非自明解が存在します．

これは における n 次多項式です．この方程式の根は行列 の 固有値 または 特性値 と呼びます．各々の固有値に対応して なる解，すなわち非自明解が存在し，それらを固有値に属する 固有ベクトル または 特性ベクトル と呼びます．方程式 (24) はまたこのようにも記述できます．

また における方程式はしばしば 特性方程式 と呼びます．

If and if is a non-singular matrix so that exists, we can solve (17) or (18) by writing

and the system has a unique solution.

Alternatively we can express the unknowns as

where , called the determinant of the system, is given by (9) and is the determinant obtained from by removing the kth column and replacing it by the column vector . The rule expressed in (20) is called Cramer’s rule.

The following four cases can arise.

Case 1, . In this case there will be a unique solution where not all will be zero.

Case 2, . In this case the only solution will be , i.e. . This is often called the trivial solution.

Case 3, . In this case there will be infinitely many solutions other than the trivial solution. This means that at least one of the equations can be obtained from the others, i.e. the equations are linearly dependent.

Case 4, . In this case infinitely many solutions will exist if and only if all of the determinants in (20) are zero. Otherwise there will be no solution.

　仮に であって更に が正則行列つまり が存在するなら，以下のように記述して (17) または (18) を解くことができます．

更にこの連立方程式は一意解を持ちます．

　代わりに未知数 を以下のように表現することもあります．

ここで は 連立方程式の行列式 と呼び， (9) により与えられまた は から k 番目の列を除去して列ベクトル に置換して与えられる行列式です．(20) に表した公式を クラメールの公式 と言います．

　下記の4つの場合が考えられます．

例 1, . この場合一意解が存在するはずで，全てでない はゼロに違いありません．

例 2, . この場合唯一の解は です．すなわち です．しばしば 自明な解 と呼びます．

例 3, . この場合自明解以外に無限に多くの解が存在するはずです．この時少なくとも一つの方程式が他の方程式から得られます．すなわちその方程式は線形従属です．

例 4, . この場合 (20) におけるすべての行列式 がゼロの時にのみ無限に多くの解が存在する筈です．他の場合は解は存在しません．

A set of equations having the form

is called a system of m linear equations in the n unknowns . If are all zero the system is called homogeneous. If they are not all zero it is called non-homogeneous. Any set of numbers which satisfies (16) is called a solution of the system.

In the matrix form (16) can be written

or more briefly

where , , represent the corresponding matrices in (17).

　以下の形式を持つ方程式の集合があるとします．

これらは n 個の未知数 についての m 個の連立方程式 と呼びます．仮に がすべてゼロならその連立方程式は 斉次 と呼びます．仮にそれらがすべてゼロでないなら 非斉次 と呼びます．(16) を満たすいかなる数 の集合も連立方程式の 解 と呼びます．

行列においては (16) の形式は以下のように記述できます．

または短縮して

ここで , , はそれぞれ (17) における対応する行列を表現しています．