日: 2013年12月18日

Partial derivatives

The partial derivatives of f(x, y) with respect to x and y are defined by

\displaystyle \frac{\partial f}{\partial x}= \lim\limits_{h \rightarrow 0} \frac{f(x + h, y) - f(x, y)}{h}\\\vspace{0.2 in} \frac{\partial f}{\partial y} = \lim\limits_{k \rightarrow 0} \frac{f(x, y + k) - f(x, y)}{k}

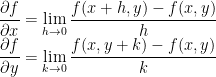
if these limits exist. It’s often written h = Δx, k = Δy. Note that \partial f/\partial x is simply the ordinary derivative of f with respect to x keeping y constant, while \partial f/\partial y is the ordinary derivative of f with respect to y keeping x constant.

Higher derivatives are defined similarly. For example, you have the second order derivatives

\displaystyle \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial^2f}{\partial x^2}\\\vspace{0.2 in} \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right) = \frac{\partial^2f}{\partial x\partial y}\\\vspace{0.2 in} \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial^2f}{\partial y\partial x}\\\vspace{0.2 in} \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right) = \frac{\partial^2f}{\partial y^2}

The deviation are sometimes denoted fx and fy. In such case fx(a, b), fy(a, b) denote these partial derivatives evaluated at (a, b).

The deviations are denoted by fxx, fxy, fyx, fyy respectively. The second and third results will be the same if f has continuous partial derivatives of second order at least.

The differentiation of f(x, y) is defined as

\displaystyle df = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy

where h = Δx = dx, k = Δy = dy.

偏微分

　x および y に対しての f(x, y) の偏導関数は次式で定義されます．

\displaystyle \frac{\partial f}{\partial x}= \lim\limits_{h \rightarrow 0} \frac{f(x + h, y) - f(x, y)}{h}\\\vspace{0.2 in} \frac{\partial f}{\partial y} = \lim\limits_{k \rightarrow 0} \frac{f(x, y + k) - f(x, y)}{k}

　しばしば h = Δx, k = Δy のように記述します．y を定数とした x に対する f の通常の導関数は単に \partial f/\partial x と記述し，一方 x を定数とした y に対する f の通常の導関数は \partial f/\partial y と記述します．

　高階の導関数もまた同様に定義します．例えば，2 階の通常の導関数は下記のようです．

\displaystyle \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial^2f}{\partial x^2}\\\vspace{0.2 in} \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right) = \frac{\partial^2f}{\partial x\partial y}\\\vspace{0.2 in} \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial^2f}{\partial y\partial x}\\\vspace{0.2 in} \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right) = \frac{\partial^2f}{\partial y^2}

　偏導関数は時々 fx や fy とも記述します．そのような場合 fx(a, b), fy(a, b) は点 (a, b) において評価されるこれらの偏微分です．

　偏導関数はまた fxx, fxy, fyx, fyy とも記述します．f が少なくとも 2 階の連続な偏微分を有するなら 2 階や 3 階微分の結果もまた同様です．

　f(x, y) の全微分は次のように定義します．

\displaystyle df = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy

　ただし h = Δx = dx, k = Δy = dy です．