日: 2013年12月21日

These represent two lines in the xy plane, and in general will meet in a point whose coordinates (x, y) are found by solving simultaneously.

It’s convenient to write these in determinant form as

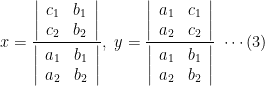
where it is defined a determinant of the second order or order 2 to be

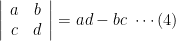
It should be noted that the denominator for x and y in (3) is the determinant consisting of the coefficients of x and y in (1). The numerator for x is found by replacing the first column of the denominator by the constants c₁, c₂ on the right side of (1). Similarly the numerator for y is found by replacing the second column of the denominator by c₁, c₂. This procedure is often called Cramer’s rule. In case the denominator in (3) is zero, the two lines represented by (1) do not meet in one point but are either coincident or parallel.

The ideas are easily extended. Thus you can consider the equations

representing 3 planes. If they intersect in a point, the coordinates (x, y, x) of this point are found from Cramer’s rule to be

where it can be defined the determinant of order 3 by

The determinant can also be evaluated in terms of second order determinants as follows

where it is noted that a₁, b₁, c₁ are the elements in the first row and the corresponding second order determinants are those obtained from the given third order determinant by removing the row and column in which the element appears.

　これらは xy 平面における 2 本の直線を示しており，一般に (x, y) 座標で交わる 1 点において同時に解が得られます．

　これを行列式で表現するのは便利です．

　2 次の行列式は次のように定義します．

　強調すべきことですが，(3) で記述した x と y の分母は (1) の x と y の係数を含む行列式です．x の分子は分母の 1 列目を (1) の右側の c₁, c₂ の定数で置換して得られます．同様に y の分子は c₁, c₂ で 2 列目を置換して得られます．この処理はしばしば Crame’s rule と呼ばれます．(3) の分母がゼロの場合は (1) で示される 2 行は1点で交差せず，一致するか平行であるかです．

　この考えは容易に拡張できます．次の方程式を考えてみましょう．

3行を示します．これらが 1 点で交わる場合，この点の (x, y, z) 座標は Cramer’s rule から得られます．

　3 次の行列式は次のように定義されます．

　この行列式は 2 次の行列式の面で次のように評価されます．

　ここで強調しておきたいことは，a₁, b₁, c₁ は 1 行目の要素であり，対応する 2 次の行列式は 3 次の行列式からその要素が現れる行と列を除去して得られます．