How to make a honeycomb grid with slave flash, black straw, and plastic cardboard?

In this article, I’d like to describe how to make a honeycomb grid, to illuminate high directive fill light from behind a model.

Purchase slave flash
Purchase materials
Assemble

1. Purchase slave flash

You can select slave flash. In this article, I’d like to select as below. The guide number is 5, it may not enough.

If you would need a flash with large guide number, you could select as below.

2. Purchase materials

The material list is following;

Black straw
Stainless steel bowl
Adhesives
Black plastic cardboard

I purchased black straw on Amazon, which diameter is 1.3 cm, for eating tapioca.

Stainless steel bowl with inner gloss surface is a reflector of flash. The diameter is 13 cm. You could select 11 cm or 18 cm diameter, depending on required size.

I purchased adhesive on 100 yen shop. You would have to purchase adhesives which could adhere polypropylene, because the straw is made from polypropylene. You should avoid superglue.

I purchased plastic cardboard on Amazon.

3. Assemble

Calculate the required number of straws
Cut straws with same length
Adhere straws
Wrap cardboard around the honeycomb

1. Calculate the required number of straws

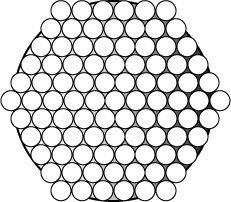
Required number of straw depends on the diameter of bowl and straw. The diameter of bowl is 13 cm and the diameter of straw is 1.3 cm, respectively. You could cover the opening of bowl with honeycomb if you had at least 10 straws diameter. It becomes hexagonal if you spread all over same size circles without gaps. If the number of circles on the line passing between a vertex and the vertex of the diagonal is odd number, we obtain regular hexagon. Now we need eleven straws. If you put the number of circles on diagonal as n, we obtain the total number of straw with calculating as following formula.

$\displaystyle N = \left\{n-1 + \frac{n + 1}{2}\right\}\times \frac{n - 1}{2} + n = \frac{3n^2 + 1}{4}$

2. Cut straws with same length

Measure the length with a ruler and cut the required number of straws. I’d like to make honeycomb with 2 cm and 4 cm thick. It may become uneven, you don’t have to care. The average length of them should be 2 cm and 4 cm from the law of great numbers.

3. Adhere straws

Adhere straws as below. It might be appropriate to set straws with required number before you adhere.

Adhere them from bottom to top with quickly.

Now you get honeycomb. Press one side of honeycomb to the work bench to align the tip before the adhesive become hard.

4. Wrap cardboard around the honeycomb

When you wrap cardboard around the honeycomb, you would have to pay attention in feature of cardboard. Cardboard has 4 mm thickness, and when you fold cardboard without incision, the folding would be distorted. It is required to bundle straws. You should put a cut inside of folding. I have purchased cardboard with 60 cm long side and 45 cm short side. To make a regular hexagonal column of 6 cm height and 8 cm side, cut out a rectangle about 6 cm and 45 cm.

You should make incision with fold along honeycomb as following picture.

After making incision, adhere straw to cardboard with adhesive as following picture.

ヒカル小町と黒ストローを使ってハニカムグリッドを自作する

　今回は黒ストローを用いてハニカムグリッドを自作する方法を述べます．太いストローや作業に適したプラダンが100円ショップで見つからず，Amazonで購入しました．目的はモデルの背後から当てるリムライトです．

ヒカル小町を購入する
材料を購入する
組み立て

1. ヒカル小町を購入する

　ヒカル小町にはいくつかの種類がありますが，今回は下記を使用することにします．ガイドナンバーは5でそれほど大きくありません．

　ガイドナンバーの大きい物が必要な場合は下記がよいでしょう．

2. 材料を購入する

　材料リストは下記の通りです．

黒ストロー
ステンレス製ボウル
接着剤
プラダン（黒）

　黒ストローは Amazon で購入しました．一般の細いストローも検討しましたが，市販のハニカムグリッドに近いほうが良いかと思われたためです．これはタピオカ用で直径 1.3 cm と通常よりかなり太いものです．

　ステンレス製のボウルは内面の光沢をストロボの反射鏡として用います．口径は 13 cm のものにしました．他には 11 cm のものや 18 cm のものもありました．用途に応じて選べばよいでしょう．

　接着剤は100円ショップで購入しました．ストローの素材はポリプロピレンなので，ポリプロピレンを接着可能なものを選びます．瞬間接着剤は避けたほうがよいでしょう．プラダンも Amazon で購入しました．

3. 組み立て

必要なストローの数を計算する
ストローを切り揃える
ストローを接着する
プラダンを巻きつけて接着する

1. 必要なストローの数を計算する

　必要なストローの本数はボウルの口径とストローの直径で決まります．今回は口径 13 cm のボウルに直径 1.3 cm のストローを用いるので，最低10本のストローでボウルの開口部を覆うことができると推測します．円を隙間なく詰めていくと六角形になるのは経験上分かります．正六角形にするには六角形のある頂点と対角の頂点を通る円の数が奇数である必要があり，今回は 11 本のストローが必要となります．この本数を n とすると，全体で必要なストローの本数 N は下式で求まります．11 本の場合は全部で 91 本が必要とわかります．

$\displaystyle N = \left\{n-1 + \frac{n + 1}{2}\right\}\times \frac{n - 1}{2} + n = \frac{3n^2 + 1}{4}$

2. ストローを切り揃える

　定規で長さを計りながら必要な本数の黒ストローをはさみで切断します．今回は 2 cm と 4 cm の二種類を作ることにします．多少不揃いになりますが問題ありません．大数の法則から平均値 2 cm および 4 cm に収束する筈です．

3. ストローを接着する

　下図のように 1 列ごとにストローを接着していきます．あらかじめ必要な本数ごとに並べておくとよいでしょう．

　下から順に積み上げて接着していきます．手早く作業を進めます．

　六角形になりました．接着剤が固まらないうちに片面を作業台に押し当てて先端位置を揃えます．多少ずれていても実用上問題はありません．

4. プラダンを巻きつけて接着する

　プラダンをストロー周囲に巻きつける際，プラダンの性質に注意する必要があります．プラダンは厚さが 4 mm あり，そのまま曲げると折り目付近に歪みが発生します．接着したストローが分解しないように補強するのが目的ですので，折り目の内側に切込みを入れておくのがよいでしょう．今回購入したプラダンは長辺 60 cm, 短辺 45 cmの製品です．一辺 8 cm 高さ 5 cm および高さ 6 cm の正六角柱を作るため，45 cm × 5 cm および 45 cm × 6 cm 程度の長方形をそれぞれ切り出します．

実物で合わせながら折り曲げていきます．仮組みしながら切込みを入れていくのがよいでしょう．写真は切り込んだ部分を表裏逆に広げたものです．

切込みと折り目づけが済んだらストローに接着剤を塗ってプラバンを接着します．この際，切り口の揃った方に合わせて下さい．写真は接着後にステンレスボウルに被せた状態で撮影したものです．

Systemic IgG4-related lymphadenopathy: a clinical and pathologic comparison to multicentric Castleman’s disease

Differential diagnosis between Castleman’s disease and systemic IgG4-related lymphadenopathy is described in this article. In their patients, systemic IgG4-related lymphadenopathy showed pathologic features only partially overlapping those of multicentric Castleman’s disease. Serum data, especially CRP and IL-6 are useful for differentiating the two.

Systemic IgG4-related lymphadenopathy: a clinical and pathologic comparison to multicentric Castleman’s disease

Yasuharu Sato, Masaru Kojima, Katsuyoshi Takata, Toshiaki Morito, Hideki Asaoku, Tamotsu Takeuchi, Kohichi Mizobuchi, Megumu Fujihara, Kazuya Kuraoka, Tokiko Nakai, Kouichi Ichimura, Takehiro Tanaka, Maiko Tamura, Yuriko Nishikawa and Tadashi Yoshino

Modern Pathology (2009) 22, 589–599

IgG4-related disease sometimes involves regional and/or systemic lymph nodes, and often clinically and/or histologically mimics multicentric Castleman’s disease or malignant lymphoma. In this study, we examined clinical and pathologic findings of nine patients with systemic IgG4-related lymphadenopathy. None of these cases were associated with human herpes virus-8 or human immunodeficiency virus infection, and there was no T-cell receptor or immunoglobulin gene rearrangement. Histologically, systemic IgG4-related lymphadenopathy was classified into two types by the infiltration pattern of IgG4-positive cells: interfollicular plasmacytosis type and intra-germinal center plasmacytosis type. The interfollicular plasmacytosis type showed either Castleman’s disease-like features or atypical lymphoplasmacytic and immunoblastic proliferation-like features. By contrast, the intra-germinal center plasmacytosis type showed marked follicular hyperplasia, and infiltration of IgG4-positive cells mainly into the germinal centers, and some cases exhibited features of progressively transformed germinal centers. Interestingly, eight of our nine (89%) cases showed eosinophil infiltration in the affected lymph nodes, and examined patients showed high elevation of serum IgE. Laboratory examinations revealed elevation of serum IgG4 and soluble interleukin-2 receptors. However, the levels of interleukin-6, C-reactive protein, and lactate dehydrogenase were within normal limits or only slightly elevated in almost all patients. One patient showed a high interleukin-6 level whereas C-reactive protein was within the normal limit. Autoantibodies were examined in five patients and detected in four. Compared with the previously reported cases of multicentric Castleman’s disease, our patients with systemic IgG4-related lymphadenopathy were significantly older and had significantly lower C-reactive protein and interleukin-6 levels. In conclusion, in our systemic IgG4-related lymphadenopathy showed pathologic features only partially overlapping those of multicentric Castleman’s disease, and serum data (especially C-reactive protein and interleukin-6) are useful for differentiating the two. Our findings of eosinophil infiltration in the affected tissue and elevation of serum IgE may suggest an allergic mechanism in the pathogenesis of systemic IgG4-related lymphadenopathy.

Keywords: systemic IgG4-related lymphadenopathy; C-reactive protein; interleukin-6; immunoglobulin E; multicentric castleman’s disease

Systemic IgG4-related lymphadenopathy: a clinical and pathologic comparison to multicentric Castleman’s disease

　キャッスルマン病と systemic IgG4-related lymphadenopathy との鑑別点について述べられています．Systemic IgG4-related lymphadenopathy の一部とキャッスルマン病とでは病理像に共通点も見られますが，CRP と IL-6 により鑑別できるとしています．

Systemic IgG4-related lymphadenopathy: a clinical and pathologic comparison to multicentric Castleman’s disease

Yasuharu Sato, Masaru Kojima, Katsuyoshi Takata, Toshiaki Morito, Hideki Asaoku, Tamotsu Takeuchi, Kohichi Mizobuchi, Megumu Fujihara, Kazuya Kuraoka, Tokiko Nakai, Kouichi Ichimura, Takehiro Tanaka, Maiko Tamura, Yuriko Nishikawa and Tadashi Yoshino

Modern Pathology (2009) 22, 589–599

IgG4 関連疾患は時に局所または全身リンパ節に浸潤し，時にキャッスルマン病や悪性リンパ腫と臨床的・組織学的に類似する．本研究では我々は systemic IgG4-related lymphadenopathy の臨床的・病理学的所見を調査した．ヒトヘルペスウイルス 8 や HIV 感染と関連した症例や，T cell receptor や免疫グロブリンの遺伝子再構成と関連した症例はなかった．組織学的には systemic IgG4-related lymphadenopathy は IgG4 陽性細胞の浸潤パターンにより 2 型に分類される．すなわち，濾胞間形質細胞型と胚中心形質細胞型に．濾胞間形質細胞型はキャッスルマン病様か異型リンパ形質細胞の像を呈し，免疫芽細胞増殖様の特徴を呈する．対照的に，胚中心形質細胞型は著明な濾胞の過形成を呈し，IgG4 陽性細胞は主に胚中心に浸潤し，ある例では進行した胚中心の形質転換像を呈していた．興味深いことに 9 例のうち 8 例で好酸球浸潤を幹部のリンパ節に認め，血清 IgE の著明な上昇を認めた．検査所見では血清 IgG4 と sIL-2R の上昇が認められた．しかしながら全症例において IL-6, CRP, LDH のレベルは正常範囲または軽度の上昇に留まった．1 名の患者は IL-6 の高値を認めたが CRP は正常範囲に留まった．自己抗体を 5 名の患者で検査し 4 名の患者で検出した．これまで報告された多中心性キャッスルマン病の症例と比較して，我々の systemic IgG4-related lymphadenopathy の患者は著明に高齢で CRP と IL-6 値が著明に低値であった．結論として我々の systemic IgG4-related lymphadenopathy は，多中心性キャッスルマン病との間に部分的に共通する病理学的特徴を有し，血清データ（特に CRP と IL-6）は両者を鑑別するのに有用であった．我々の所見は患部組織への好酸球浸潤と血清 IgE 上昇であるが，systemic IgG4-related lymphadenopathy の病原性においてアレルギー的な機序を示唆するのかもしれない．

Keywords: systemic IgG4-related lymphadenopathy; C-reactive protein; interleukin-6; immunoglobulin E; multicentric castleman’s disease

Numerical methods for solving differential equations

Given the boudary-value problem
$\displaystyle dy/dx = f(x, y)\ \ \ y(x_0) = y_0\ \ \ (1)$
it may not be possible to obtain an exact solution. In such case various methods are available for obtaining an approximate or numerical solution. In the following we list several methods.

Step by step or Euler method

Taylor series method

Picard’s method

Runge-Kutta method

1. Step by step or Euler method

In this method we replace the differential equation of (1) by the approximation
$\displaystyle \frac{y(x_0 + h)-y(x_0)}{h} = f(x_0, y_0)\ \ \ (2)$
so that
$\displaystyle y(x_0 + h) = y(x_0) + hf(x_0, y_0)\ \ \ (3)$
By continuity in this manner we can then find $y(x_0 + 2h),\ y(x_0 + 3h)$ , etc. We choose $h$ sufficiently small so as to obtain good approximations.

A modified procedure of this method can also be used.

2. Taylor series method

By successive differentiation of the differential equation in (1) we can find $y'(x_0),\ y''(x_0),\ y'''(x_0),\cdots$ . Then the solution is given by the Taylor series
$\displaystyle y(x) = y(x_0) + y'(x_0)(x - x_0) + \frac{y''(x_0)(x - x_0)^2}{2!} + \cdots\ \ \ (4)$
assuming that the series converges. If it does we can obtain $y(x_0 + h)$ to any desired accuracy.

3. Picard’s method

By integrating the differential equation in (1) and using the boundary condition, we find
$\displaystyle y(x) = y_0 + \int^{x}_{x_0}\! f(u, y)du\ \ \ (5)$
Assuming the approximation $y_1(x) = y_0$ , we obtain from (5) a new approximation.
$\displaystyle y_2(x) = y_0 + \int^{x}_{x_0}\! f(u, y_1)du\ \ \ (6)$
Using this in (5) we obtain another approximation.
$\displaystyle y_3(x) = y_0 + \int^{x}_{x_0}\! f(u, y_2)du\ \ \ (7)$
Continuing in this manner we obtain a sequence of approximations $y_1, y_2, y_3,\cdots$ . The limit of this sequence, if it exists, is the required solution. However, by carrying out the procedure a few times, good approximations can be obtained.

4. Runge-Kutta method

This method consists of computing
$\displaystyle \left.\begin{array}{rcl}k_1 & = & hf(x_0, y_0) \\ k_2 & = & hf(x_0 + \frac{1}{2}h, y_0 + \frac{1}{2}k_1) \\ k_3 & = & hf(x_0 + \frac{1}{2}h, y_0 + \frac{1}{2}k_2 \\ k_4 & = & hf(x_0 + \frac{1}{2}h, y_0 + \frac{1}{2}k_3) \end{array} \right\}\ \ \ (8)$
Then
$\displaystyle y(x_0 + h) = y_0 + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4)\ \ \ (9)$
These methods can also be adapted for higher order differential equations by writing them as several first order equations.

微分方程式を解くための数値解法

　次の境界値問題が与えられたとします．

$\displaystyle dy/dx = f(x, y)\ \ \ y(x_0) = y_0\ \ \ (1)$

恐らく正確な解を得ることはできないでしょう．このような場合，様々な方法で近似値や数値解法が得られます．いくつかの方法を列挙します．

逐次近似法またはオイラー法
テイラー級数法
ピカール法
ルンゲクッタ法

1. 逐次近似法またはオイラー法

　この手法では微分方程式 (1) を次の近似式で置換します．

$\displaystyle \frac{y(x_0 + h)-y(x_0)}{h} = f(x_0, y_0)\ \ \ (2)$

そのため，

$\displaystyle y(x_0 + h) = y(x_0) + hf(x_0, y_0)\ \ \ (3)$

このような連続性により $y(x_0 + 2h),\ y(x_0 + 3h)$ 等を見出すことができます．十分に小さな $h$ を選ぶことで良い近似が得られます．

　この方法の変法もまた用いられています．

2. テイラー級数法

　(1) における微分方程式を連続して微分することで $y'(x_0),\ y''(x_0),\ y'''(x_0),\cdots$ が得られます．そしてその解は，その級数が収束することを前提に，次のテイラー級数で得られます．

$\displaystyle y(x) = y(x_0) + y'(x_0)(x - x_0) + \frac{y''(x_0)(x - x_0)^2}{2!} + \cdots\ \ \ (4)$

級数が収束するならいかなる精度でも $y(x_0 + h)$ が得られます．

3. ピカール法

　(1) の微分方程式を積分し，境界条件を用いることで次式が得られます．

$\displaystyle y(x) = y_0 + \int^{x}_{x_0}\! f(u, y)du\ \ \ (5)$

近似式 $y_1(x) = y_0$ を前提として (5) から次の新しい近似式が得られます．

$\displaystyle y_2(x) = y_0 + \int^{x}_{x_0}\! f(u, y_1)du\ \ \ (6)$

(5) においてこれを用いると別の近似式が得られます．

$\displaystyle y_3(x) = y_0 + \int^{x}_{x_0}\! f(u, y_2)du\ \ \ (7)$

　このように連続して一連の近似式 $y_1, y_2, y_3,\cdots$ を得ます．この一連の近似式の極限は，もし存在するなら，求められる解です．しかしながら数回の手順を行うことで良い近似が得られます．

4. ルンゲクッタ法

　この手法は次の計算を含みます．

$\displaystyle \left.\begin{array}{rcl}k_1 & = & hf(x_0, y_0) \\ k_2 & = & hf(x_0 + \frac{1}{2}h, y_0 + \frac{1}{2}k_1) \\ k_3 & = & hf(x_0 + \frac{1}{2}h, y_0 + \frac{1}{2}k_2 \\ k_4 & = & hf(x_0 + \frac{1}{2}h, y_0 + \frac{1}{2}k_3) \end{array} \right\}\ \ \ (8)$

　ゆえに

$\displaystyle y(x_0 + h) = y_0 + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4)\ \ \ (9)$

　これらの手法もまた数個の1階の微分方程式として記述することで高階の微分方程式に適合しています．

How to make a sunuto with Hikaru-Komachi and available materials in 100 yen shop?

In this article, I’d like to describe how to make sunuto with slave flash and available materials in 100 yen shop. Hikaru-Komachi, the light quantity doesn’t reach the studio flash, is slave flash that the position of them is fill light.

Purchase slave flash
Purchase the materials in 100 yen shop
Assemble

1. Purchase slave flash

You can select slave flash from many choice. Hikaru-Komachi 2D requires two AA batteries and its guide number is 5 fixed. If you need larger guide number, you can select Hikaru-Komachi Di (GN 13) or other slave flash.

2. Purchase the materials in 100 yen shop

Required materials are following list;

Plastic tape with wire
Packing tape
Stainless steel bowl
Aluminum sheet for thermal insulation

I purchased plastic tape with wire at horticultural corner and stainless steel bowl at kitchen corner, respectively. Inner gloss surface is a reflector of flash. I purchased aluminum sheet at special event corner.

3. Assemble

Cut aluminium sheet to appropriate size and wrap it around the bowl, and fix with packing tape. The exact form of the aluminum sheet is fan-shaped. If you cut it into a rectangular shape, you don’t have to care. You can adjust the margin.

Cut the packing tape with length of the opening of the bowl and paste the plastic tape along the packing tape. The wire is for keeping the opening circular shape.

Paste packing tape with plastic tape around the opening of the column of aluminium sheet.

Put slave flash into the bowl. Finished!

Now, calculate the performance of the fill light. If you would shoot with medium-size or large-size format, you might set aperture of lens to 16 or 22. If you set aperture to 16 with GN 5, for example, you can get correct exposure with shooting distance 33 cm. If you use the sunuto as fill light, you have to close to 8 cm. If you use flash with GN 13, you can get correct exposure with 75 cm distance and fill light effect with 19 cm, respectively. The light quantity is not enough. You might set the distance at least 50 cm between model and sunuto. You might require GN 32 flash with aperture 16 and GN 44 flash with aperture 22, respectively.

100円ショップとヒカル小町でスヌートを自作する

　今回はヒカル小町および 100 円ショップで揃えた物品を用いてスヌートを自作する方法を述べます．ヒカル小町はスレーブ専用ストロボで，光量や使い勝手は大光量のスタジオ用のストロボには及びません．あくまでも補助光源としての位置付けです．トップからのヘアライト，主光源のバンクやアンブレラは完成しており，リムライトとしてモデルの背後から当てる目的です．

ヒカル小町を購入する
100円ショップで材料を購入する
組み立て

1. ヒカル小町を購入する

　ヒカル小町には様々なバリエーションがあります．今回は最新のものを使用することにします．電源は単3電池2本でガイドナンバーは5に固定されています．

2. 100円ショップで材料を購入する

　必要な物品は下記のとおりです．

ワイヤー入りビニール紐
ガムテープ（黒）
ステンレス製野菜入れ
アルミ保温シート

　ワイヤー入りビニール紐は園芸コーナーにありました．ステンレス製野菜入れはキッチンコーナーにあり，コップのような形をしています．内面の光沢を反射鏡として用います．アルミ保温シートは催事コーナーにありました．数10cm四方あれば十分です．

3. 組み立て

　アルミ保温シートを適当な大きさに切ってステンレス製野菜入れに巻きつけ，ガムテープで止めます．アルミ保温シートの形状は厳密には扇形になりますが，長方形でも重ね合わせる糊代で調整すれば問題ありません．

　開口部の円周の長さにガムテープを切り，ワイヤー入りビニール紐を長めに切って貼り付けます．このワイヤーは開口部の形状を維持するためのものです．

　ワイヤー入りビニール紐を貼り付けたガムテープを開口部に貼り付けます．余ったワイヤー入りビニール紐は切り落とします．

　中にヒカル小町を入れて完成です．覗きこんでみると上記のようになります．

　ところで，ガイドナンバーから実際にフィルライトとしての性能を計算してみます．中版や大判カメラの場合絞りはかなり絞って撮影します．例えば絞り16の場合，上記ガイドナンバーですと撮影距離は 5/16 ≅ 1/3, つまり約 33 cm で適正です．フィルライトとして使うならその 4 分の 1 の距離，つまり 8 cm ほどまで近づける必要があります．ガイドナンバー 13 の製品の場合ですと適正距離は 13/16 ≅ 0.75 m, フィルライトとして使うなら 19 cm まで近づける必要があります．光量が足りませんね．モデルの背後に置くための物品などの取り合わせからすると最低でも 0.5 m は離す必要があります．逆算すると絞り 16 でガイドナンバー 32, 絞り 22 でガイドナンバー 44 が必要です．きちんとしたスレーブストロボを考慮すべきでしょう．

Special first order equations and solutions

Any first order differential equation can be put into the form
$\displaystyle \frac{dy}{dx} = f(x,y)$
or
$\displaystyle M(x,y)dx + N(x,y)dy = 0$
and the general solution of such an equation contains one arbitrary constant. Many special devices are available for finding general solutions of various types of first order differential equations. In the following list some of types are given.

Separation of variables

Exact equation

Integrating factor

Linear equation

Homogeneous equation

Bernoulli’s equation

Equation solvable for y

Clairaut’s equation

Miscellaneous equations

1. Separation of variables

If differential equation is given as below,
$\displaystyle f_1(x)g_1(y)dx + f_2(x)g_2(y)dy = 0$
divide by $g_1(y)f_2(x) \ne 0$ and integrate to obtain general solution
$\displaystyle \int\frac{f_1(x)}{f_2(x)}dx + \int\frac{g_2(y)}{g_1(y)}dy = c$
2. Exact equation

If differential equation is given as below,
$\displaystyle M(x, y)dx + N(x, y)dy = 0$
where $\displaystyle \frac{\partial M}{\partial y} = \frac{\partial N}{\partial x}$

The equation can be written as
$\displaystyle Mdx + Ndy = dU(x, y) = 0$
where dU is an exact differential. Thus the solution is $U(x, y) = c$ or equivalently
$\displaystyle \int M\partial x + \int\left(N - \frac{\partial}{\partial y}\int M\partial x\right)dy = c$
where δx indicates that the integration is to be performed with respect to x keeping y constant.

3. Integrating factor

If differential equation is given as below,
$\displaystyle M(x, y)dx + N(x, y)dy = 0$
where
$\displaystyle \frac{\partial M}{\partial y} \neq \frac{\partial N}{\partial x}$
The equation can be written as an exact differential equation
$\displaystyle \mu M dx + \mu N dy = 0$
where μ is an appropriate integrating factor.

The following combination are often useful in finding integration factors.

$\displaystyle \frac{xdy - ydx}{x^2} = d\left(\frac{y}{x}\right)$
$\displaystyle \frac{xdy - ydx}{y^2} = -d\left(\frac{x}{y}\right)$
$\displaystyle \frac{xdy - ydx}{x^2 + y^2} = d\left(\tan^{-1}\frac{y}{x}\right)$
$\displaystyle \frac{xdy - ydx}{x^2 - y^2} = \frac{1}{2}d\left(\ln\frac{x - y}{x + y}\right)$
$\displaystyle \frac{xdx + ydy}{x^2 + y^2} = \frac{1}{2}d\{\ln(x^2 + y^2)\}$

4. Linear equation

If differential equation is given as below,
$\displaystyle \frac{dy}{dx} + P(x)y = Q(x)$
An integrating factor is given by
$\displaystyle \mu = e^{\int P(x)dx}$
and the equation can then be written
$\displaystyle \frac{d}{dx}(\mu y) = \mu Q$
with solution
$\displaystyle \mu y = \int \mu Qdx + c$
or
$\displaystyle ye^{\int Pdx} = \int Qe^{\int Pdx}dx + c$
5. Homogeneous equation

If differential equation is given as below,
$\displaystyle \frac{dy}{dx} = F\left(\frac{y}{x}\right)$
Let $y/x = v$ or $y = vx$ , and the equation becomes
$\displaystyle v + x\frac{dv}{dx} + F(x)$
or
$\displaystyle xdv + (F(x) - v)dx = 0$
which is of Type 1 and has the solution
$\displaystyle \ln x = \int \frac{dv}{F(v) - v} + c$
where $v = y/x$ . If $F(v) = v$ , the solution is $y = cx$ .

6. Bernoulli’s equation

If differential equation is given as below,
$\displaystyle \frac{dy}{dx} + P(x)y = Q(x)y^n,\ n \neq 0, 1$
Letting $v = y^{1 - n}$ , the equation reduces to Type 4 with solution
$\displaystyle ve^{(1-n)\int Pdx} = (1 - n)\int Qe^{(1-n)\int Pdx}dx + c$
If n = 0, the equation is of Type 4. If n = 1, it is of Type 1.

7. Equation solvable for y

If differential equation is given as below,
$\displaystyle y = g(x, y)$
where
$\displaystyle p = y'$
Differentiate both sides of the equation with respect to x to obtain
$\displaystyle \frac{dy}{dx} = \frac{dg}{dx} = \frac{\partial g}{\partial x} + \frac{\partial g}{\partial p}\frac{\partial p}{\partial x}$
or
$\displaystyle p = \frac{\partial g}{\partial x} + \frac{\partial g}{\partial p}\frac{\partial p}{\partial x}$
Then solve this last equation to obtain $G(x, p, c) = 0$ . The required solution is obtained by eliminating p between $G(x, p, c) = 0$ and $y = g(x, p)$ .

An analogous method exists if the equation is solvable for x.

8. Clairaut’s equation

If differential equation is given as below,
$\displaystyle y = px + F(p)$
where
$\displaystyle p = y'$
The equation is of Type 7 and has solution
$\displaystyle y = cx + F(c)$
The equation will also have a singular solution in general.

9. Miscellaneous equations

If differential equation is given as below,
$\displaystyle (a) \frac{dy}{dx} = F(\alpha x + \beta y)\\\vspace{0.2 in} (b) \frac{dy}{dx} = F\left(\frac{\alpha_1 x + \beta_1 y + \gamma_1}{\alpha_2 x + \beta_2 y + \gamma_2}\right)$
(a)Letting $\alpha x + \beta y = v$ , the equation reduces Type 1.

(b)Let $x = X +h,\ y = Y + k$ and choose constants h and k so that the equation reduces to Type 5. This is possible if and only if $\alpha_1/\alpha_2 \neq \beta_1/\beta_2$ . If $\alpha_1/\alpha_2 = \beta_1/\beta_2$ , the equation reduces to Type 9(a).

特殊な1階常微分方程式とその解

　いかなる 1 階の微分方程式も次の形に置き換えることができます．

$\displaystyle \frac{dy}{dx} = f(x,y)$

または

$\displaystyle M(x,y)dx + N(x,y)dy = 0$

そしてそれらの方程式の一般解は一つの任意定数を持ちます．様々な種類の 1 階微分方程式の一般解の発見には多くの特殊な装置が有用です．下記のリストにはその幾つかを示してあります．

変数分離法
完全微分方程式
積分因子
線形微分方程式
同次方程式
ベルヌーイの方程式
y について解ける方程式
クレローの方程式
その他の方程式

1. 変数分離法

　微分方程式が下記のようである場合は

$\displaystyle f_1(x)g_1(y)dx + f_2(x)g_2(y)dy = 0$

一般解を得るには $g_1(y)f_2(x) \ne 0$ で除し，積分します．

$\displaystyle \int\frac{f_1(x)}{f_2(x)}dx + \int\frac{g_2(y)}{g_1(y)}dy = c$

2. 完全微分方程式

　微分方程式が下記のようである場合は

$\displaystyle M(x, y)dx + N(x, y)dy = 0$

ここで $\displaystyle \frac{\partial M}{\partial y} = \frac{\partial N}{\partial x}$

　この方程式は次のように書き換えられます．

$\displaystyle Mdx + Ndy = dU(x, y) = 0$

ここで dU は完全微分方程式です．ゆえにその解は $U(x, y) = c$ または同等の解として

$\displaystyle \int M\partial x + \int\left(N - \frac{\partial}{\partial y}\int M\partial x\right)dy = c$

ここで δx は y を定数とし x による積分を行うことを示します．

3. 積分因子

　微分方程式が下記のようである場合，

$\displaystyle M(x, y)dx + N(x, y)dy = 0$

ここで

$\displaystyle \frac{\partial M}{\partial y} \neq \frac{\partial N}{\partial x}$

　この方程式は次のように完全微分方程式に書き換えられます．

$\displaystyle \mu M dx + \mu N dy = 0$

ここで μ は適切な積分因子です．

　下記の組み合わせは積分因子を発見するのにしばしば有用です．

$\displaystyle \frac{xdy - ydx}{x^2} = d\left(\frac{y}{x}\right)$
$\displaystyle \frac{xdy - ydx}{y^2} = -d\left(\frac{x}{y}\right)$
$\displaystyle \frac{xdy - ydx}{x^2 + y^2} = d\left(\tan^{-1}\frac{y}{x}\right)$
$\displaystyle \frac{xdy - ydx}{x^2 - y^2} = \frac{1}{2}d\left(\ln\frac{x - y}{x + y}\right)$
$\displaystyle \frac{xdx + ydy}{x^2 + y^2} = \frac{1}{2}d\{\ln(x^2 + y^2)\}$

4. 線形微分方程式

　微分方程式が下記のようである場合，

$\displaystyle \frac{dy}{dx} + P(x)y = Q(x)$

　積分因子は次のように得られます．

$\displaystyle \mu = e^{\int P(x)dx}$

また方程式は次のように書き換えられます．

$\displaystyle \frac{d}{dx}(\mu y) = \mu Q$

解は以下のようです．

$\displaystyle \mu y = \int \mu Qdx + c$

または

$\displaystyle ye^{\int Pdx} = \int Qe^{\int Pdx}dx + c$

5. 同次方程式

微分方程式が下記のようである場合，

$\displaystyle \frac{dy}{dx} = F\left(\frac{y}{x}\right)$

　 $y/x = v$ または $y = vx$ とします．すると方程式は次のようになります．

$\displaystyle v + x\frac{dv}{dx} + F(x)$

または

$\displaystyle xdv + (F(x) - v)dx = 0$

ここで Type 1 と同じになり，解は次のようになります．

$\displaystyle \ln x = \int \frac{dv}{F(v) - v} + c$

ここで $v = y/x$ です．もし $F(v) = v$ なら解は $y = cx$ となります．

6. ベルヌーイの方程式

微分方程式が下記のようである場合，

$\displaystyle \frac{dy}{dx} + P(x)y = Q(x)y^n,\ n \neq 0, 1$

　 $v = y^{1 - n}$ とします．すると方程式は Type 4 に置き換えられ，解は次のようになります．

$\displaystyle ve^{(1-n)\int Pdx} = (1 - n)\int Qe^{(1-n)\int Pdx}dx + c$

　仮に n = 0 なら方程式は Type 4 と同じであり， n = 1 なら Type 1 と同じです．

7. y について解ける方程式

　微分方程式が下記のようである場合，

$\displaystyle y = g(x, y)$

ここで

$\displaystyle p = y'$

　方程式の両辺を x について微分すると次が得られます．

$\displaystyle \frac{dy}{dx} = \frac{dg}{dx} = \frac{\partial g}{\partial x} + \frac{\partial g}{\partial p}\frac{\partial p}{\partial x}$

または

$\displaystyle p = \frac{\partial g}{\partial x} + \frac{\partial g}{\partial p}\frac{\partial p}{\partial x}$

　そしてこの最後の方程式を解くと $G(x, p, c) = 0$ が得られます．必要な解は $G(x, p, c) = 0$ と $y = g(x, p)$ の間の p を消去して得られます．

　その方程式を x について解くための類似の方法が存在します．

8. クレローの方程式

　微分方程式が下記のようである場合，

$\displaystyle y = px + F(p)$

ここで

$\displaystyle p = y'$

　この方程式は Type 7 に置き換えられ，解は次の通りです．

$\displaystyle y = cx + F(c)$

　この方程式もまた一般解のうち単解を有します．

9. その他の方程式

微分方程式が下記のようである場合，

$\displaystyle (a) \frac{dy}{dx} = F(\alpha x + \beta y)\\\vspace{0.2 in} (b) \frac{dy}{dx} = F\left(\frac{\alpha_1 x + \beta_1 y + \gamma_1}{\alpha_2 x + \beta_2 y + \gamma_2}\right)$

(a) $\alpha x + \beta y = v$ とすると，方程式は Type 1 に置き換えられます．

(b) $x = X +h,\ y = Y + k$ とし，定数 h と k を方程式が Type 5 に置き換えられるように定めます．この処理は以下の場合，すなわち $\alpha_1/\alpha_2 \neq \beta_1/\beta_2$ の場合に限り可能です．仮に $\alpha_1/\alpha_2 = \beta_1/\beta_2$ の場合，方程式は Type 9(a) に置き換えられます．

月	火	水	木	金	土	日
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31