日: 2014年3月4日

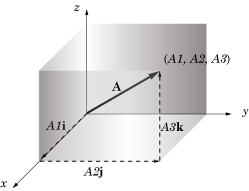
Components of a vector

Any vector \bold{A} in 3 dimensions can be represented with initial point at the origin O of a rectangular coordinate system. Let (A_1, A_2, A_3) be the rectangular coordinates of the terminal point of vector \bold{A} with initial point at O. The vectors A_1\bold{i}, A_2\bold{j} and A_3\bold{k} are called the rectangular component vectors, or simply component vectors, of \bold{A} in the x, y and z directions respectively. A_1, A_2 and A_3 are called the rectangular components, or simply components, of \bold{A} in the x, y and z directions respectively.

The sum or resultant of A_1\bold{i}, A_2\bold{j} and A_3\bold{k} is the vector \bold{A}, so that we can write

\bold{A} = A_1\bold{i} + A_2\bold{j} + A_3\bold{k}\cdots(1)

The magnitude of \bold{A} is

A = |\bold{A}| = \sqrt{A_1^2 + A_2^2 + A_3^2}\cdots(2)

In particular, the position vector or radius vector \bold{r} from O to the point (x, y, z) is written

\bold{r} = x\bold{i} + y\bold{j} + z\bold{k}\cdots(3)

and has magnitude r = |\bold{r}| = \sqrt{x^2 + y^2 + z^2}.

Vector

ベクトルの成分

　3次元におけるいかなるベクトル \bold{A} も直交座標系の原点 O における始点により表現可能です．ここでベクトル \bold{A} を直交座標系における原点 O を始点とし (A_1, A_2, A_3) を終点としましょう．そのベクトル A_1\bold{i}, A_2\bold{j} および A_3\bold{k} はそれぞれ \bold{A} における x, y および z 軸方向の 直交成分ベクトル, あるいは単に 成分ベクトル といいます．A_1, A_2 および A_3 はそれぞれ x, y および z 軸方向における \bold{A} の 直交成分, または単に 成分 と呼ばれます．

　A_1\bold{i}, A_2\bold{j} および A_3\bold{k} の和や結果が \bold{A} であり，ゆえに

\bold{A} = A_1\bold{i} + A_2\bold{j} + A_3\bold{k}\cdots(1)

　\bold{A} の大きさは

A = |\bold{A}| = \sqrt{A_1^2 + A_2^2 + A_3^2}\cdots(2)

　特に，原点 O から点 (x, y, z) への 位置ベクトル または 動径ベクトル \bold{r} は以下のように記述できます．

\bold{r} = x\bold{i} + y\bold{j} + z\bold{k}\cdots(3)

またその大きさは r = |\bold{r}| = \sqrt{x^2 + y^2 + z^2} となります．

Vector