A simple closed curve is a curve which does not intersect itself anywhere. Mathematically, a curve in the 
plane is defined by the parametric equations 
where 
and 
are single-valued and continuous in an interval 
. If 
and 
, the curve is said to be closed. If 
and 
only when 
(except in the special case where 
and 
), the curve is closed and does not intersect itself and so is a simple closed curve. We shall also assume, unless otherwise stated, that 
and 
are piecewise differentiable in .
If a plane region has the property that any closed curve in it can be continuously shrunk to a point without leaving the region, then the region is called simply-connected, otherwise it is called multiply-connected.
As the parameter 
varies from 
to 
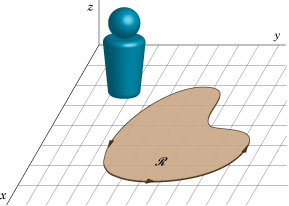
, the plane curve is described in a certain sense or direction. For curves in the plane, we arbitrarily describe this direction as positive or negative according as a person traversing the curve in this direction with his head pointing in the positive 
direction has the region enclosed by the curve always toward his left or right respectively. If we look down upon a simple closed curve in the plane, this amounts to saying that traversal of the curve in the counterclockwise direction is taken as positive while traversal in the clockwise direction is taken as negative.
