ロジスティック回帰分析においては確率pをオッズ p/(1-p) に変換し，更にオッズの対数（ロジット）を取って回帰分析を行います．この意味を少し考えました．元々は二項分布と言って，ある目的とする事象が起きるか起きないかいずれかの値しか取らない現象を重回帰分析するために考えだされた方法です．世界恐慌直後の米国である疫学調査が行われ，その際に考案された手法だとされています．
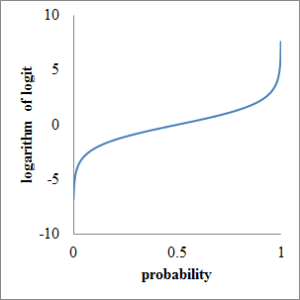
確率 p は 0 から 1 の範囲でしか値を取りません．これをマイナス無限大からプラス無限大の範囲に拡張するのがロジットです．グラフを見たほうが分かりやすいでしょう．
確率pは 0 以上 1 以下の実数です．横軸を p, 縦軸を 
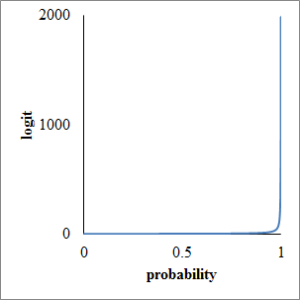
次に横軸にオッズ，縦軸に対数オッズ（ロジット）を取ってグラフを描くと下図のようになります．対数オッズ（ロジット）の範囲がマイナス無限大からプラス無限大に拡張しました．
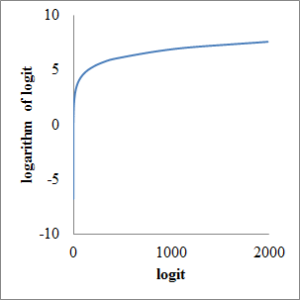
最後に横軸にp, 縦軸に対数オッズ（ロジット）を取ってグラフを描くと下図のようになります．0 から 1 の範囲しか取れなかった確率 p が，対数オッズ（ロジット）に変換されることでマイナス無限大からプラス無限大までの実数に拡張したことが分かります．
![\displaystyle \begin{array} {rcl} P &=& \frac{(a+b)!(c+d)!(a+c)!(b+d)!}{N!a!b!c!d!}\vspace{0.2in}\\&=& \exp\left[LN \left( \frac{(a+b)!(c+d)!(a+c)!(b+d)!}{N!a!b!c!d!} \right) \right]\vspace{0.2in}\\ &=& \exp [LN((a+b)!) +LN((c+d)!) +LN((a+c)!) +LN((b+d)!)\vspace{0.2in}\\& & -LN(N!) -LN(a!) -LN(b!) -LN(c!) -LN(d!) ]\end{array}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cbegin%7Barray%7D+%7Brcl%7D+P+%26%3D%26+%5Cfrac%7B%28a%2Bb%29%21%28c%2Bd%29%21%28a%2Bc%29%21%28b%2Bd%29%21%7D%7BN%21a%21b%21c%21d%21%7D%5Cvspace%7B0.2in%7D%5C%5C%26%3D%26+%5Cexp%5Cleft%5BLN+%5Cleft%28+%5Cfrac%7B%28a%2Bb%29%21%28c%2Bd%29%21%28a%2Bc%29%21%28b%2Bd%29%21%7D%7BN%21a%21b%21c%21d%21%7D+%5Cright%29+%5Cright%5D%5Cvspace%7B0.2in%7D%5C%5C+%26%3D%26+%5Cexp+%5BLN%28%28a%2Bb%29%21%29+%2BLN%28%28c%2Bd%29%21%29+%2BLN%28%28a%2Bc%29%21%29+%2BLN%28%28b%2Bd%29%21%29%5Cvspace%7B0.2in%7D%5C%5C%26+%26+-LN%28N%21%29+-LN%28a%21%29+-LN%28b%21%29+-LN%28c%21%29+-LN%28d%21%29+%5D%5Cend%7Barray%7D&bg=T&fg=000000&s=0 "\displaystyle \begin{array} {rcl} P &=& \frac{(a+b)!(c+d)!(a+c)!(b+d)!}{N!a!b!c!d!}\vspace{0.2in}\\&=& \exp\left[LN \left( \frac{(a+b)!(c+d)!(a+c)!(b+d)!}{N!a!b!c!d!} \right) \right]\vspace{0.2in}\\ &=& \exp [LN((a+b)!) +LN((c+d)!) +LN((a+c)!) +LN((b+d)!)\vspace{0.2in}\\& & -LN(N!) -LN(a!) -LN(b!) -LN(c!) -LN(d!) ]\end{array}")