有効か無効か,生存か死亡かなどの値が TRUE か FALSE の二項分布する名義変数をアウトカムとし,危険因子の暴露ありかなしか,介入ありかなしか,実薬か偽薬かなどの値が POSITIVE か NEGATIVE の二項分布する名義変数を予知因子とする場合,四分表により予知因子がアウトカムに及ぼす影響が統計的有意か否かをオッズ比や相対危険度の95%信頼区間により判定できます.
オッズ比は症例対照研究に用いられ,オッズ比が1だと予知因子は何の効果もないことになります.オッズ比が1より大きいと予知因子によるアウトカムの発生が増えることになります.逆に1より小さければアウトカムの発生を抑制することになります.
相対危険度は前向きコホート試験やランダム化比較試験で用いられ,1より大きければ予知因子はアウトカムの発生を高め,1より小さければ予知因子はアウトカムの発生が低くなることになります.
オッズ比,相対危険度共に95%信頼区間が1を跨いでいる場合には統計的有意とはいえません.
| |
TRUE |
FALSE |
Marginal total |
| POSITIVE |
a |
b |
a + b |
| NEGATIVE |
c |
d |
c + d |
| Marginal total |
a + c |
b + d |
N |
オッズ比ORは以下の式で求まります.
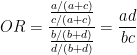
オッズ比の95%信頼区間は以下の式で求まります.

相対危険度RRは以下の式で求まります.
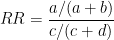
相対危険度の95%信頼区間は以下の式で求まります.
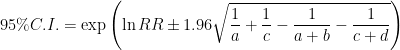
; Average, SE; standard error, SD; standard deviation
