You can determine statistically significance with Odds ratio, relative risk and 95% confidence interval by two-by-two table which treats such binomial values which called as outcome as true or false, for example, enabled or disabled and death or survival and such binomial values which called as predictor as positive or negative, for example, with intervention or without, with exposure risk factor or without and active drug or placebo.
Odds ratio (OR) is used for case control study. When OR is 1, the predictor has no effect. When OR is greater than 1, the predictor has positive effect to outcome. If it is smaller than 1, the predictor has opposite effect to outcome.
Relative risk (RR) is used for prospective cohort study and randomized controlled trials. It means that when RR is greater than 1 the predictor has positive effect to outcome and when RR is smaller than 1 the predictor has negative effect to outcome.
If 1 is between lower bound and upper bound of 95% confidence interval of Odds ratio and relative risk, it is not statistically significant.
| |
TRUE |
FALSE |
Marginal total |
| POSITIVE |
a |
b |
a + b |
| NEGATIVE |
c |
d |
c + d |
| Marginal total |
a + c |
b + d |
N |
You could calculate Odds ratio and 95% confidence interval with formula below;
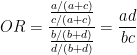

You could calculate relative risk and 95% confidence interval with formula below;
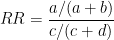
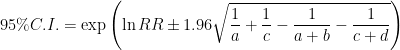
; Average, SE; standard error, SD; standard deviation
