タグ: force field

CONDITIONS FOR A LINE INTEGRAL TO BE INDEPENDENT OF THE PATH

  • Theorem 6-1.

    • A necessary and sufficient condition for \displaystyle \int_C [Pdx + Qdy] to be independent of the path C joining any two given points in a region \cal R is that in \cal R

    \partial P/\partial y = \partial Q/\partial x\cdots (23)

    where it is supposed that these partial derivatives are continuous in \cal R.

The condition (23) is also the condition that Pdx + Qdy is an exact differential, i.e. that there exists a function \phi(x, y) such that Pdx + Qdy = d\phi. In such case if the end points of curve C are (x_1, y_1) and (x_2, y_2), the value of the line integral is given by

\displaystyle \int_{(x_1, y_1)}^{(x_2, y_2)}[Pdx + Qdy] = \int_{(x_1, y_1)}^{(x_2, y_2)} d\phi = \phi(x_2, y_2) - \phi(x_1, y_1) \cdots(24)

In particular if (23) holds and C is closed, we have x_1 = x_2,\ y_1 = y_2 and

\displaystyle \oint_C [Pdx + Qdy] = 0\cdots(25)

The results in Theorem 6-1 can be extended to line integrals in space. Thus we have

  • Theorem 6-2.

    • A necessary and sufficient condition for \displaystyle \int_C [A_1dx + A_2dy + A_3dz] to be independent of the path C joining any two given points in a region \cal R is that in \cal R

    \displaystyle \frac{\partial A_1}{\partial y} = \frac{\partial A_2}{\partial x},\ \frac{\partial A_3}{\partial x} = \frac{\partial A_1}{\partial z},\ \frac{\partial A_2}{\partial z} = \frac{\partial A_3}{\partial y} \cdots(26)

    where it is supposed that these partial derivatives are continuous in \cal R.

The results can be expressed concisely in terms of vectors. If \bold{A} = A_1\bold{i} + A_2\bold{j} + A_3\bold{k} , the line integral can be written \displaystyle \int_C \bold{A}\cdot d\bold{r} and condition (26) is equivalent to the condition \nabla \times \bold{A} = 0. If \bold{A} represents a force field \bold{F} which acts on an object, the result is equivalent to the statement that the work done in moving the object from one point to another is independent of the path joining the two points if and only if \nabla \times \bold{A} = 0. Such a force field is often called conservative.

The condition (26) [or the equivalent condition \nabla\times\bold{A}=0] is also the condition that A_1dx + A_2dy + A_3dz [or \bold{A}\cdot\bold{r}] is an exact differential, i.e. that there exists a function \phi(x, y, z) such that A_1dx + A_2dy + A_3dz =d\phi. In such case if the endpoints of curve C are (x_1, y_1, z_1) and (x_2, y_2, z_2), the value of the line integral is given by

\displaystyle \int_{(x_1, y_1, z_1)}^{(x_2, y_2, z_2)}\bold{A}\cdot\bold{r} = \int_{(x_1, y_1, z_1)}^{(x_2, y_2, z_2)}d\phi = \phi(x_2, y_2, z_2)- \phi(x_1, y_1, z_1)\cdots(27)

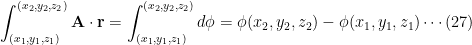
In particular if C is closed and \nabla\times\bold{A} = 0, we have

\displaystyle \oint_C \bold{A}\cdot d\bold{r} = 0 \cdots(28)

VECTOR NOTATION FOR LINE INTEGRALS

It is often convenient to express a line integral in vector form as an aid in physical or geometric understanding as well as for brevity of notation. For example, we can express the line integral (15) in the form

\displaystyle \int_{C}[A_1dx + A_2dy + A_3dz] \\ = \int_{C} (A_1\bold{i} + A_2\bold{j} + A_3\bold{k}) \cdot (dx\bold{i} + dy\bold{j} + dz\bold{k})\\ = \int_{C} \bold{A}\cdot d\bold{r} \cdots (17)

where \bold{A} = A_1\bold{i} + A_2\bold{j} + A_3\bold{k} and d\bold{r} = dx\bold{i} + dy\bold{j} + dz\bold{k}. The line integral (14) is a special case of this with z = 0.

If at each point (x, y, z) we associate a force F acting on an object (i.e. if a force field is defined), then

\displaystyle \int_{C} \bold{F}\cdot d\bold{r}\cdots(18)

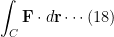
represents physically the total work done in moving the object along the curve C.