投稿者: admin

趣味：写真撮影とデータベース． カメラ：TOYO FIELD, Hasselblad 500C/M, Leica M6． SQL Server 2008 R2, MySQL, Microsoft Access．

ASCII文字コード(0-127)一覧表

　ASCII 文字セットのコードと文字を示します．正規表現の文字列パターンを設定する際に参考にして下さい．コード番号 8, 9, 10, 13 はそれぞれ制御文字でバックスペース，タブ，ラインフィード，キャリッジリターンとして用いられ，画面には表示されません．コード番号 128 から 255 まではラテン文字中心の文字コードです．

　正規表現での半角英数字の文字クラスは [a-zA-Z0-9] のパターンで表現しますが，半角記号だとやや長くなり，[!-/:-@[-`{-~] となります．文字クラス内でエスケープが必要な文字は ] と \ だけです．

Code Character Meta character
0    
1    
2    
3    
4    
5    
6    
7    
8 *1  
9 *2  
10 *3  
11    
12    
13 *4  
14    
15    
16    
17    
18    
19    
20    
21    
22    
23    
24    
25    
26    
27    
28    
29    
30
–
  
31    
32 [space]   
33 !   
34 ”   
35 #   
36 $   
37 %   
38 &   
39 ‘   
40 (  ✔
41 )  ✔
42 *  ✔
43 +  ✔
44 ,   
45 –   
46 .  ✔
47 /   
48 0   
49 1   
50 2   
51 3   
52 4   
53 5   
54 6   
55 7   
56 8   
57 9   
58 :   
59 ;   
60 <   
61 =   
62 >   
63 ?  ✔
64 @   
65 A   
66 B   
67 C   
68 D   
69 E   
70 F   
71 G   
72 H   
73 I   
74 J   
75 K   
76 L   
77 M   
78 N   
79 O   
80 P   
81 Q   
82 R   
83 S   
84 T   
85 U   
86 V   
87 W   
88 X   
89 Y   
90 Z   
91 [  ✔
92 \  ✔
93 ]  ✔
94 ^  ✔
95 _   
96 `   
97 a   
98 b   
99 c   
100 d   
101 e   
102 f   
103 g   
104 h   
105 i   
106 j   
107 k   
108 l   
109 m   
110 n   
111 o   
112 p   
113 q   
114 r   
115 s   
116 t   
117 u   
118 v   
119 w   
120 x   
121 y   
122 z   
123 {  ✔
124 |  ✔
125 }  ✔
126 ~   
127    

参照：ASCII文字コード

How to get first cell which is referred to formula and last cell which refers to formula in Excel worksheet?

In the situation that you had to parse worksheet with much formula, what would you do? You would trace formula to first cell which has no reference. In this article, I’d like to describe to find the first cells with wading through spaghetti formula.

In order to demonstrate that set A is equal to set B, you should demonstrate that the union is equal to the intersection.

When you compare DirectPrecendents property and Precendents property, which refer to direct reference range and all reference range, respectively, if the former is equal to the later, the range is the first cell. It’s assumed that no range refers to other worksheets and they have no cyclic references.

You could constitute tree structure from first cell to last cell or from the last to the first, respectively. It’s a common technique to configure deployment folders or components. 

Option Explicit
Sub FirstPrecedents()
    Dim Sh1 As Worksheet
    Dim Sh2 As Worksheet
    Dim i   As Long
    Dim tmp As Range
    Set Sh1 = ActiveSheet
    Set Sh2 = Worksheets.Add
    Sh2.Name = "TraceFormula"
    i = 1
    For Each tmp In Sh1.UsedRange
        On Error Resume Next
        If Left(tmp.Formula, 1) = "=" Then
            If CheckEqualRange(tmp.DirectPrecedents, tmp.Precedents) Then
                With Sh2
                    .Cells(i, 1) = tmp.Address
                    .Cells(i, 2) = "'" & tmp.Formula
                    .Cells(i, 3) = tmp.DirectPrecedents.Address
                    .Cells(i, 4) = tmp.Precedents.Address
                    .Cells(i, 5) = tmp.DirectPrecedents.Cells.Count
                    .Cells(i, 6) = tmp.Precedents.Cells.Count
                    .Cells(i, 7) = CheckEqualRange(tmp.DirectPrecedents, tmp.Precedents)
                End With
                tmp.DirectPrecedents.Interior.Color = RGB(242, 220, 219)
                i = i + 1
            End If
        End If
        On Error GoTo 0
    Next tmp
End Sub

Function CheckEqualRange(ByRef Rng1 As Range, ByRef Rng2 As Range) As Boolean
    Dim UnionRange      As Range
    Dim IntersectRange  As Range
    Dim tmp             As Range
    CheckEqualRange = False
    Set UnionRange = Application.Union(Rng1, Rng2)
    Set IntersectRange = Application.Intersect(Rng1, Rng2)
    If UnionRange.Cells.Count = IntersectRange.Cells.Count Then
        CheckEqualRange = True
    End If
End Function

I’d like to present other code with DirectDependents property and DirectPrecedents property of range object. It’s the first cell that the range has DirectDependents property but has no DirectPrecedents property. 

Option Explicit
Sub FirstPrecedents2()
    Dim Sh1 As Worksheet
    Dim Sh2 As Worksheet
    Dim i   As Long
    Dim tmp As Range
    Set Sh1 = ActiveSheet
    Set Sh2 = Worksheets.Add
    Sh2.Name = "Root"
    i = 1
    For Each tmp In Sh1.UsedRange
        On Error Resume Next
        If Left(tmp.Formula, 1) = "=" Then
            If tmp.DirectPrecedents Is Nothing And _
               Not tmp.DirectDependents Is Nothing Then
                Sh2.Cells(i, 1) = tmp.Address
                i = i + 1
            End If
        End If
        On Error GoTo 0
    Next tmp
End Sub

At last, I’d like to present the code to get the last cells that have opposite Boolean value of conditional expression. 

Option Explicit
Sub LastDependents()
    Dim Sh1 As Worksheet
    Dim Sh2 As Worksheet
    Dim i   As Long
    Dim tmp As Range
    Set Sh1 = ActiveSheet
    Set Sh2 = Worksheets.Add
    Sh2.Name = "Leaf"
    i = 1
    For Each tmp In Sh1.UsedRange
        On Error Resume Next
        If Left(tmp.Formula, 1) = "=" Then
            If tmp.DirectDependents Is Nothing And _
                Not tmp.DirectPrecedents Is Nothing Then
                tmp.Interior.Color = RGB(220, 230, 241)
                Sh2.Cells(i, 1) = tmp.Address
                i = i + 1
            End If
        End If
        On Error GoTo 0
    Next tmp
End Sub

EXCELワークシートにおいて数式の参照元の最初のセルおよび参照先の最後のセルを取得する

　数式の参照元セルが多数存在するワークシートを解析しなければならない場合があります．大抵の場合，一つのセルが他のセルの参照元となっていて，かつ別のセルの参照先になっていることが殆どです．参照元の更に参照元を辿って行くと，それ以上は参照元のない最初のセルに行き着きます．今回の記事ではその最初の参照元のセルを探すコードを紹介します．

　2 つの集合が等しいかを確認する方法を用います．ある集合 A と B とが等しいと証明するには，集合 A と集合 B の和と積とをとります．和集合 A ∪ B と積集合 A ∩ B との要素数が等しければ集合 A と集合 B は等しいと言えます．

　比較する対象は Range オブジェクトの DirectPrecedents プロパティと Precedents プロパティです．それぞれセルの直接参照元と参照元全てを取得するプロパティであり，それらが一致すれば参照元が最初のセルとなります．前提条件として他のワークシートへの参照がなく，循環参照を使用していないものとします．

　セルの参照元と参照先を全て繋ぐと木構造になります．最初の参照元，最後の参照先，どちらのルートから辿っても木構造ができます．構成展開で再帰的にノードを展開し，今回作成した関数でリーフか否かを判定します．フォルダや部品表の展開などで一般的に用いられる手法です．

Option Explicit
Sub FirstPrecedents()
    Dim Sh1 As Worksheet
    Dim Sh2 As Worksheet
    Dim i   As Long
    Dim tmp As Range
    Set Sh1 = ActiveSheet
    Set Sh2 = Worksheets.Add
    Sh2.Name = "TraceFormula"
    i = 1
    For Each tmp In Sh1.UsedRange
        On Error Resume Next
        If Left(tmp.Formula, 1) = "=" Then
            If CheckEqualRange(tmp.DirectPrecedents, tmp.Precedents) Then
                With Sh2
                    .Cells(i, 1) = tmp.Address
                    .Cells(i, 2) = "'" & tmp.Formula
                    .Cells(i, 3) = tmp.DirectPrecedents.Address
                    .Cells(i, 4) = tmp.Precedents.Address
                    .Cells(i, 5) = tmp.DirectPrecedents.Cells.Count
                    .Cells(i, 6) = tmp.Precedents.Cells.Count
                    .Cells(i, 7) = CheckEqualRange(tmp.DirectPrecedents, tmp.Precedents)
                End With
                tmp.DirectPrecedents.Interior.Color = RGB(242, 220, 219)
                i = i + 1
            End If
        End If
        On Error GoTo 0
    Next tmp
End Sub

Function CheckEqualRange(ByRef Rng1 As Range, ByRef Rng2 As Range) As Boolean
    Dim UnionRange      As Range
    Dim IntersectRange  As Range
    Dim tmp             As Range
    CheckEqualRange = False
    Set UnionRange = Application.Union(Rng1, Rng2)
    Set IntersectRange = Application.Intersect(Rng1, Rng2)
    If UnionRange.Cells.Count = IntersectRange.Cells.Count Then
        CheckEqualRange = True
    End If
End Function

　もう一つの方法として，Range オブジェクトの DirectDependents プロパティと DirectPrecedents プロパティを比較する方法もあります．DirectPrecedents プロパティが存在せず，DirectDependents プロパティが存在すればそれはルートであるということです．

Option Explicit
Sub FirstPrecedents2()
    Dim Sh1 As Worksheet
    Dim Sh2 As Worksheet
    Dim i   As Long
    Dim tmp As Range
    Set Sh1 = ActiveSheet
    Set Sh2 = Worksheets.Add
    Sh2.Name = "Root"
    i = 1
    For Each tmp In Sh1.UsedRange
        On Error Resume Next
        If Left(tmp.Formula, 1) = "=" Then
            If tmp.DirectPrecedents Is Nothing And _
               Not tmp.DirectDependents Is Nothing Then
                Sh2.Cells(i, 1) = tmp.Address
                i = i + 1
            End If
        End If
        On Error GoTo 0
    Next tmp
End Sub

　ついでに参照先の最後のセルを取得するコードも紹介しておきます．条件式の真理値を逆転させるだけです．

Option Explicit
Sub LastDependents()
    Dim Sh1 As Worksheet
    Dim Sh2 As Worksheet
    Dim i   As Long
    Dim tmp As Range
    Set Sh1 = ActiveSheet
    Set Sh2 = Worksheets.Add
    Sh2.Name = "Leaf"
    i = 1
    For Each tmp In Sh1.UsedRange
        On Error Resume Next
        If Left(tmp.Formula, 1) = "=" Then
            If tmp.DirectDependents Is Nothing And _
                Not tmp.DirectPrecedents Is Nothing Then
                tmp.Interior.Color = RGB(220, 230, 241)
                Sh2.Cells(i, 1) = tmp.Address
                i = i + 1
            End If
        End If
        On Error GoTo 0
    Next tmp
End Sub

How to validate empty value in controls on user form of Excel VBA?

In this article, I’d like to describe how to validate empty value in controls on UserForm of Excel VBA. It’s list of controls that you can select and enter on form.

  • CheckBox
  • OptionButton
  • ComboBox
  • ListBox
  • TextBox

It’s assumed that OptionButtons and CheckBoxes are placed in Frame and they aren’t placed within one Frame together.

UserForm1

It is needed to designe as public function that validates empty value.

The function that validates empty value of controls on forms is called from multiple CommandButtons. Therefore, it’s reasonable to design as public function. It’s needed to add module for implementing the function. Data type of return value is Variant as following code because it returns name list of empty controls as string. It may be Boolean if you don’t have to present message box. 

Option Explicit

Function CheckControls(myForm As MSForms.UserForm) As Variant
    Dim Ctrl        As MSForms.Control
    Dim CheckCnt    As Long
    Dim myCnt       As Long
    Dim CheckStr    As String
    CheckControls = False
    CheckCnt = 0
    myCnt = 0
    CheckStr = ""
    For Each Ctrl In myForm.Controls
        Select Case TypeName(Ctrl)
            Case "ComboBox"
                If Ctrl.ListIndex <> -1 Then
                    myCnt = myCnt + 1
                Else
                    CheckStr = CheckStr & Ctrl.Name & vbCrLf
                End If
            Case "Frame"
                If CheckFrame(Ctrl) Then
                    myCnt = myCnt + 1
                Else
                    CheckStr = CheckStr & Ctrl.Name & vbCrLf
                End If
            Case "ListBox"
                If Ctrl.ListIndex <> -1 Then
                    myCnt = myCnt + 1
                Else
                    CheckStr = CheckStr & Ctrl.Name & vbCrLf
                End If
            Case "TextBox"
                If Ctrl.Text <> "" Then
                    myCnt = myCnt + 1
                Else
                    CheckStr = CheckStr & Ctrl.Name & vbCrLf
                End If
            Case Else
                CheckCnt = CheckCnt - 1
        End Select
        CheckCnt = CheckCnt + 1
    Next Ctrl
    If CheckCnt = myCnt Then
        CheckControls = True
    Else
        CheckControls = CheckStr
    End If
End Function

Function CheckFrame(myFrame As MSForms.Frame) As Boolean
    Dim FrmCnt  As Long
    Dim ChkCnt  As Long
    Dim OptCnt  As Long
    Dim tmpCtrl As Control
    CheckFrame = False
    FrmCnt = 0
    ChkCnt = 0
    OptCnt = 0
    For Each tmpCtrl In myFrame.Controls
        Select Case TypeName(tmpCtrl)
            Case "CheckBox"
                If tmpCtrl.Value Then
                    ChkCnt = ChkCnt + 1
                End If
            Case "OptionButton"
                If tmpCtrl.Value Then
                    OptCnt = OptCnt + 1
                End If
        End Select
    Next tmpCtrl
    FrmCnt = FrmCnt + 1
    If FrmCnt = OptCnt Or FrmCnt <= ChkCnt Then
        CheckFrame = True
    End If
End Function

The code that calls the function

You would write the code on click event as below. You could write the procedure between "If ... Then" and "Else" statements that is activated when it has passed verification. 

Option Explicit

Private Sub CommandButton1_Click()
    If TypeName(CheckControls(Me)) = "Boolean" Then
        
    Else
        MsgBox Prompt:=CheckControls(Me) & "Missing value above.", Title:="Empty values!"
        Exit Sub
    End If
End Sub

CheckBox could take NULL

To tell the truth, CheckBox has interesting property. Although OptionButton tekes only TRUE or FALSE, CheckBox takes three-valued logic with NULL. It's very difficult problem for database designers because NULL brings them unexpected results in query. Three-valued logic is the greatest weakness of relational model. TripleState property, its default value is FALSE, could select whether three-valued logic would be allowed or not.

It's assumed that one or more controls are checked in Frame. If the procedure validates naked CheckBox without Frame, what happens? Whatever the value of CheckBox is, it passes verification. You shouldn't use three-valued logic to select TURE or FALSE only.

Three-valued logic and set of choices

Furthermore, to allow multiple choices means that users would be allowed to not select any options more. Relation of 1:0 and 1:n are allowed, respectively. Fortunately, the situation could be avoided with careful design of choices. It's needed to be carefully treated of "Other case" that couldn't be treated as number. It's impossible to isolate and salvage data that is classified as "Others".

References:
Userform of Excel VBA as user interface
Three-valued logic (Wikipedia)

EXCEL VBA でユーザーフォーム上のコントロールの未入力を検証する

　今回はフォーム上のコントロールの形式的検証のうち，未入力のコントロールをチェックするコードを紹介します．フォーム上に入力・選択可能なコントロールとしては以下が挙げられます．

  • チェックボックス
  • オプションボタン
  • コンボボックス
  • リストボックス
  • テキストボックス

　オプションボタンおよびチェックボックスはフレーム内に配置してあるものとし，一つのフレーム内にオプションボタンとチェックボックスは混在していないと仮定しています．

UserForm1

未入力のコントロールを検証する関数を共通化する

　フォーム上のコントロールの未入力のチェックは複数のコマンドボタンから共通して呼び出される機能であるため，共通化したほうがコーディングの重複をなくせます．そのため標準モジュールを追加して関数として実装することにします．下記の関数で戻り値を Variant 型にしているのは未入力のコントロール名を文字列型で受けているためです．メッセージボックスを表示する必要がなければ戻り値を Boolean 型にした方がよいでしょう．また Select case 節でコントロールの種類を群別しているため case else 節でコントロール数を減算する処理を追加していますが，If … Then … ElseIf … 節で群別すればその記述は不要になります．

Option Explicit

Function CheckControls(myForm As MSForms.UserForm) As Variant
    Dim Ctrl        As MSForms.Control
    Dim CheckCnt    As Long
    Dim myCnt       As Long
    Dim CheckStr    As String
    CheckControls = False
    CheckCnt = 0
    myCnt = 0
    CheckStr = ""
    For Each Ctrl In myForm.Controls
        Select Case TypeName(Ctrl)
            Case "ComboBox"
                If Ctrl.ListIndex <> -1 Then
                    myCnt = myCnt + 1
                Else
                    CheckStr = CheckStr & Ctrl.Name & vbCrLf
                End If
            Case "Frame"
                If CheckFrame(Ctrl) Then
                    myCnt = myCnt + 1
                Else
                    CheckStr = CheckStr & Ctrl.Name & vbCrLf
                End If
            Case "ListBox"
                If Ctrl.ListIndex <> -1 Then
                    myCnt = myCnt + 1
                Else
                    CheckStr = CheckStr & Ctrl.Name & vbCrLf
                End If
            Case "TextBox"
                If Ctrl.Text <> "" Then
                    myCnt = myCnt + 1
                Else
                    CheckStr = CheckStr & Ctrl.Name & vbCrLf
                End If
            Case Else
                CheckCnt = CheckCnt - 1
        End Select
        CheckCnt = CheckCnt + 1
    Next Ctrl
    If CheckCnt = myCnt Then
        CheckControls = True
    Else
        CheckControls = CheckStr
    End If
End Function

Function CheckFrame(myFrame As MSForms.Frame) As Boolean
    Dim FrmCnt  As Long
    Dim ChkCnt  As Long
    Dim OptCnt  As Long
    Dim tmpCtrl As Control
    CheckFrame = False
    FrmCnt = 0
    ChkCnt = 0
    OptCnt = 0
    For Each tmpCtrl In myFrame.Controls
        Select Case TypeName(tmpCtrl)
            Case "CheckBox"
                If tmpCtrl.Value Then
                    ChkCnt = ChkCnt + 1
                End If
            Case "OptionButton"
                If tmpCtrl.Value Then
                    OptCnt = OptCnt + 1
                End If
        End Select
    Next tmpCtrl
    FrmCnt = FrmCnt + 1
    If FrmCnt = OptCnt Or FrmCnt <= ChkCnt Then
        CheckFrame = True
    End If
End Function

コマンドボタンに関数を呼び出すコードを記述する

　フォーム上のコマンドボタンには下記のコードを記述します．If ... Then 節には入力値の検証に合格した際の動作を記述します．

Option Explicit

Private Sub CommandButton1_Click()
    If TypeName(CheckControls(Me)) = "Boolean" Then
        
    Else
        MsgBox Prompt:=CheckControls(Me) & "上記項目が未入力です", Title:="未入力エラー"
        Exit Sub
    End If
End Sub

チェックボックスは NULL を取りうる

　さて，実はチェックボックスには面白い性質があります．オプションボタンでは TRUE と FALSE の 2 値しか取りませんが，チェックボックスの場合は更に NULL を加えた 3 値の真理値を取ることができます．しかしデータベース設計者にとって NULL は極めて扱いの難しい真理値であり，クエリが予想外の結果を返すことがあるためなるべく NULL を許容すべきではありません．3 値論理は関係モデルにとって急所なのです．TripleState プロパティで 3 値論理を認めるか否か変更できます．既定値は FALSE となっています．一方でオプションボタンにはそのようなプロパティは存在しません．

　上記の例文ではフレーム内のチェックボックスやリストボックスの選択肢から最低でも 1 つ選択されている，という前提でチェックをかけています．では，フレーム内ではなくフォーム上にチェックボックスが存在する場合はどうでしょうか．この場合，チェックボックスの値にかかわらず検証はパスします．ですが TRUE か FALSE かを必ず選択させるために 3 値論理を導入するのは行き過ぎかと思います．

3 値論理と選択肢の設定

　さらにチェックボックス，リストボックスいずれにも言えることですが，複数選択を許可するということは，どの選択肢も選択しないことをも許容することを意味します．つまり関係モデル上 1:n のリレーションのうち n = 0 も成り立つということです．とは言え，選択肢を注意深く設定することである程度は回避可能です．例えば年齢を 10 歳区分で区切る場合に両端の年代をどのように扱うかや，年収を 100 万円単位で区切る場合に最小群と最大群をどう設定するかなどです．数値で扱えない選択項目の場合，「その他」をどこまで許容するか，慎重に設計しなければなりません．一旦「その他」に放り込まれたデータを後から切り分けて取り出すことは不可能です．必要な項目を網羅した上でこれ以上はどう考えても不要である場合にのみ「その他」とする，つまり漏れがないように選択肢を設定すべきです．

参照：
インターフェースとしてのEXCEL VBAによるユーザーフォーム
Three-valued logic (Wikipedia)

How to execute formal validation of TextBox on user form with EXCEL VBA?

In this article, I’d like to describe how to execute formal validation of TextBox on user form. Data type of TextBox is datetime, numeric and such string as zip code, phone number or mail address, etc. Until Excel 2003, you could divert calendar control of Access®, but after 2007, you couldn’t. You might have to type keyboard, design custom calendar or use Add-In calendar.

validation

As shown in figure above, set TextBoxes on user form, from TextBox1 to TextBox5. And set CommandButton.

Formal validation

Validation means formal validation and semantic validation. In this article, I’d like to describe about formal validation. Formal validation has verification of data type and not entered controls. You could verify not entered controls at last, it might be executed in a batch, when CommandButton for registration was clicked. However, because data type of each controls are different from each other, it might be appropriate to verify data type each time when input is entered.

Semantic validation

Although I would not describe about semantic validation in this article, it’s needed not only verifying input of one control, but also comparing input of multiple controls each other and compareing input with record in database. In the situation, it’s needed to execute validation when registration button was clicked, not to hook individual events of each controls.

Event type

Then, which event should you use? When user have entered incorrect input, you would not confirm input and would not move focus to the next control. Therefore it’s appropriate to use event with cancel. Typical event of TextBox is bellow.

  • BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)
  • Change()
  • Exit(ByVal Cancel As MSForms.ReturnBoolean)
  • KeyDown(ByVal KeyCode As MSForms.ReturnInteger, ByVal Shift As Integer)
  • KeyPress(ByVal KeyAscii As MSForms.ReturnInteger)
  • KeyUp(ByVal KeyCode As MSForms.ReturnInteger, ByVal Shift As Integer)

Events with cancel process are BeforeUpdate and Exit. With such other events as Change, you would have to design custom code to stop process. BeforeUpdate event is usually used. 

Option Explicit

Private Sub TextBox1_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)

End Sub

Private Sub TextBox2_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)

End Sub

Private Sub TextBox3_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)

End Sub

Private Sub TextBox4_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)

End Sub

Private Sub TextBox5_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)

End Sub

Specified criteria for validation

It’s important that BeforeUpdate event executes cancel process when criteria you described in event procedure has been satisfied. It’s needed to deny criteria expression with Not that allows to input. When criteria has been satisfied, cancel process would be executed.

Validation of data type

Data type of each TextBoxes are datetime, numeric and string. String has mobile phone number, mail address and URL, respectively. After cancel process, following code set focus and select whole input string. In TextBox1, following code verifies whether data type of input is datetime, in textBox2, the code verifies whether data type of input is numeric, respectively. In textBox2, non-negative number would be accepted.

Validation with regular expression

After TextBox3, following code doesn’t verify data type. It’s not needed to verify data type when you deal input as string. Therefore, you would have to verify string itself. In TextBox3, it is allowed to input eleven digit number. In TextBox4, it’s allowed to input string by matching with regular expression as shown in 44 line. It’s so difficult to match e-mail address that following code is incomplete. In TextBox5, it matches with URL. As well as e-mail, it’s incomplete. 

Private Sub TextBox1_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)
    With TextBox1
        If Not IsDate(.Text) Then
            Cancel = True
            .SetFocus
            .SelStart = 0
            .SelLength = Len(.Text)
        End If
    End With
End Sub

Private Sub TextBox2_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)
    With TextBox2
        If Not (IsNumeric(.Text) And .Text >= 0) Then
            Cancel = True
            .SetFocus
            .SelStart = 0
            .SelLength = Len(.Text)
        End If
    End With
End Sub

Private Sub TextBox3_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)
    Dim myReg       As Object
    Set myReg = CreateObject("VBScript.RegExp")
    With myReg
        .Pattern = "^[0-9]{11}$"
        .IgnoreCase = True
        .Global = True
    End With
    With TextBox3
        If Not myReg.Test(.Text) Then
            Cancel = True
            .SetFocus
            .SelStart = 0
            .SelLength = Len(.Text)
        End If
    End With
End Sub

Private Sub TextBox4_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)
    Dim myReg       As Object
    Dim Pattern     As String
    Pattern = "^[-a-z0-9]+(\.[-a-z0-9]+)*\@[-a-z0-9]+(\.[-a-z0-9]+)*\.[a-z0-9]{2,6}$"
    Set myReg = CreateObject("VBScript.RegExp")
    With myReg
        .Pattern = Pattern
        .IgnoreCase = True
        .Global = True
    End With
    With TextBox4
        If Not myReg.Test(.Text) Then
            Cancel = True
            .SetFocus
            .SelStart = 0
            .SelLength = Len(.Text)
        End If
    End With
End Sub

Private Sub TextBox5_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)
    Dim myReg       As Object
    Dim Pattern     As String
    Set myReg = CreateObject("VBScript.RegExp")
    Pattern = "^https?://[a-z0-9][-a-z0-9]{0,62}(\.[a-z0-9][-a-z0-9]{0,62})*\.[a-z0-9][a-z0-9]{0,62}$"
    With myReg
        .Pattern = Pattern
        .IgnoreCase = True
        .Global = True
    End With
    With TextBox5
        If Not myReg.Test(.Text) Then
            Cancel = True
            .SetFocus
            .SelStart = 0
            .SelLength = Len(.Text)
        End If
    End With
End Sub

Refferences:
DOD INTERNET HOST TABLE SPECIFICATION
Requirements for Internet Hosts — Application and Support
Hostname (Wikipedia)
Userform of Excel VBA as user interface

Excel VBAでユーザーフォームのテキストボックスの値の形式的検証を行う

　ユーザーフォーム上のテキストボックスの値を検証します．テキストボックスに入力する値のデータ型としては日付型，数値型，郵便番号や電話番号・メールアドレスなどの文字列型が主体です．日付型に関しては Excel 2003 までは Access® のカレンダーコントロールを流用できたのですが，最近のバージョンではそれもできなくなりました．キーボードからタイプするか，カレンダーを自作するか，関数アドインを利用するしかありません．

validation

　上図のようにフォーム上にテキストボックスを配置します．それぞれ TextBox1, TextBox2, TextBox3, TextBox4, TextBox5 としましょう．またコマンドボタンを配置し，Caption を OK に変更します．

形式的検証

　検証には形式的検証と意味的検証とがあります．まず形式的検証についてです．未入力のチェックとデータ型のチェックが主体となります．両者のチェックのタイミングは別の方がよいでしょう．タイミングが異なるため，異なるイベントにすべきです．未入力のチェックは値が空白であるか否かだけを確認すれば良いため，一括して検証可能でしょう．となると個々のコントロールのイベントで都度チェックするのではなく，最後に登録するコマンドボタンが押された時点でよいということになります．逆にデータ型はコントロールごとに異なります．ですので個々のテキストボックスに入力が発生した時点で都度検証するのがよいでしょう．

意味的検証

　意味的検証についてここでは詳述しませんが，単独のコントロールの入力値を検証するだけでなく，複数のコントロールの入力値同士を比較して検証する必要があったり，データベースに既に登録されたレコードの値と比較したりといった検証が必要になる場合もあります．そのような場合には個々のコントロールのイベントをフックするのではなく，最後に登録するボタンが押された時点で検証するのが妥当だと思います．そういったチェックは Access® の場合ですとテーブルに対するイベントとして登録する必要があります．

イベントの種類

　話をイベントに戻します．では次にどのイベントを用いるべきでしょうか．意図しない入力が発生した場合は入力を確定させず，次のコントロールにフォーカスを移動させたくないのですから，Cancel 処理が入っているイベントが適切です．テキストボックスのイベントで代表的なものは下記のとおりです．

  • BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)
  • Change()
  • Exit(ByVal Cancel As MSForms.ReturnBoolean)
  • KeyDown(ByVal KeyCode As MSForms.ReturnInteger, ByVal Shift As Integer)
  • KeyPress(ByVal KeyAscii As MSForms.ReturnInteger)
  • KeyUp(ByVal KeyCode As MSForms.ReturnInteger, ByVal Shift As Integer)

　Cancel 処理を持つのは BeforeUpdate と Exit です．Change イベントを始め他のイベントでは処理を止めるために自前でコーディングする必要があるでしょう．BeforeUpdate と Exit とでいずれが適切かは個々の要件によりますが，通常は BeforeUpdate でよいでしょう．それぞれのコントロールで BeforeUpdate イベントを選択した状態は下記のようになります．

Option Explicit

Private Sub TextBox1_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)

End Sub

Private Sub TextBox2_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)

End Sub

Private Sub TextBox3_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)

End Sub

Private Sub TextBox4_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)

End Sub

Private Sub TextBox5_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)

End Sub

検証の条件指定

　次にデータ型をそれぞれ検証します．ここで強調したいのは，キャンセルする際の条件を満たした場合にキャンセル処理を行うコードを記述することです．その条件には，逆に入力を許可する条件式を指定しておき，最後に Not で条件式全体を否定するというちょっと複雑な処理が必要です．If … Then … ElseIf … と条件分岐を連ねていく方法もありますが，その都度キャンセル処理を書き連ねていく必要があります．ここは好みの問題かもしれませんが，ド・モルガンの法則からすると，And で条件を絞り込み，最後に Not で式全体を否定するのがスマートかと思います．そして Cancel = True としてキャンセル処理を実行します．では逆に入力を満たす条件をそのまま記述し，Cancel = False とすればどうなるでしょうか．これは宿題にしておきましょう．

データ型の検証

　さて，話を戻します．各テキストボックスのデータ型は順に日付型，数値型，電話番号・メールアドレスおよび URL の文字列型です．TextBox1 から TextBox5 までいずれもキャンセル処理後フォーカスを残し，かつ入力した値全体を選択して即座にタイプできるようにしています．TextBox2 では非負の数値のみを受け付けます．

正規表現による文字列の検証

　TextBox3 以降ではデータ型の検証をしていません．文字列型として扱う場合はデータ型を検証する必要がないからです．したがって入力された文字列そのものを検証する必要があります．TextBox3 では 11 桁の半角数値以外の入力を許可していません．TextBox4　においては正規表現を使って 44 行目のようにパターンにマッチさせる文字列を指定します．メールアドレスの正規表現によるマッチングはかなり複雑らしく，例文では不十分です．TextBox5 では URL にマッチさせます．メールアドレス同様，例文の検証法も不十分です．

Private Sub TextBox1_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)
    With TextBox1
        If Not IsDate(.Text) Then
            Cancel = True
            .SetFocus
            .SelStart = 0
            .SelLength = Len(.Text)
        End If
    End With
End Sub

Private Sub TextBox2_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)
    With TextBox2
        If Not (IsNumeric(.Text) And .Text >= 0) Then
            Cancel = True
            .SetFocus
            .SelStart = 0
            .SelLength = Len(.Text)
        End If
    End With
End Sub

Private Sub TextBox3_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)
    Dim myReg       As Object
    Set myReg = CreateObject("VBScript.RegExp")
    With myReg
        .Pattern = "^[0-9]{11}$"
        .IgnoreCase = True
        .Global = True
    End With
    With TextBox3
        If Not myReg.Test(.Text) Then
            Cancel = True
            .SetFocus
            .SelStart = 0
            .SelLength = Len(.Text)
        End If
    End With
End Sub

Private Sub TextBox4_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)
    Dim myReg       As Object
    Dim Pattern     As String
    Pattern = "^[-a-z0-9]+(\.[-a-z0-9]+)*\@[-a-z0-9]+(\.[-a-z0-9]+)*\.[a-z0-9]{2,6}$"
    Set myReg = CreateObject("VBScript.RegExp")
    With myReg
        .Pattern = Pattern
        .IgnoreCase = True
        .Global = True
    End With
    With TextBox4
        If Not myReg.Test(.Text) Then
            Cancel = True
            .SetFocus
            .SelStart = 0
            .SelLength = Len(.Text)
        End If
    End With
End Sub

Private Sub TextBox5_BeforeUpdate(ByVal Cancel As MSForms.ReturnBoolean)
    Dim myReg       As Object
    Dim Pattern     As String
    Set myReg = CreateObject("VBScript.RegExp")
    Pattern = "^https?://[a-z0-9][-a-z0-9]{0,62}(\.[a-z0-9][-a-z0-9]{0,62})*\.[a-z0-9][a-z0-9]{0,62}$"
    With myReg
        .Pattern = Pattern
        .IgnoreCase = True
        .Global = True
    End With
    With TextBox5
        If Not myReg.Test(.Text) Then
            Cancel = True
            .SetFocus
            .SelStart = 0
            .SelLength = Len(.Text)
        End If
    End With
End Sub

参照：
サイト URL、フォルダ名、ファイル名に使用できない文字 (Microsoft®)
Active Directory 内のコンピューター、ドメイン、サイト、および Ou の名前付け規則 (Microsoft®)
ホスト名 (Wikipedia)
インターフェースとしてのEXCEL VBAによるユーザーフォーム

Userform of Excel VBA as user interface

I’d like to describe about coding of userform in EXCEL VBA as user interface of database. You could set controls for entering data, selecting from choices, and coding procedure, etc. I would be happy with your help if you could understand the characteristics of controls and design a convenient and robust system.

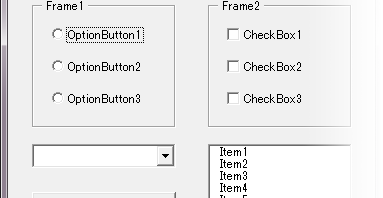
  1. OptionButton, CheckBox, ListBox and ComboBox as a choice
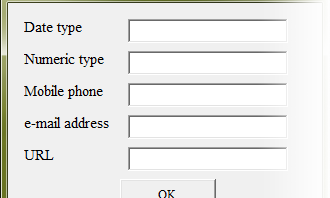
  2. TextBox
  3. CommandButton
  4. Password

1. OptionButton, CheckBox, ListBox and ComboBox as a choice

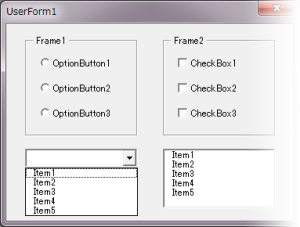
ExampleForm

1.1 Restriction which control should you select.

You might had to decide which control should you set on userform depending on the situation. First, number of choice is most important. Can you only choose one option? Or are you permitted multiple choices? Next, is there enough area to present the choices? Last, does user have to enter additional choice? Or does administrator have to define the choices?

1.2 Can you select only one? Or are you allowed to select multiple choice?

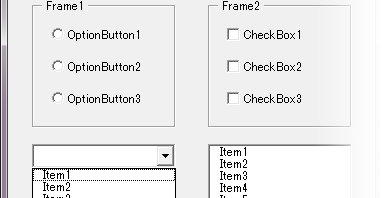
If choice was one, you could set OptionButtons in Frame or ComboBox. If you need multiple choices, you could set CheckBoxes in Frame or ListBox. I’d like to draw your attention here that multiple selection doesn’t mean unique value and doesn’t become candidate key to identify record in database. It isn’t first normal form because it is array rather than atomic value.

1.3 Enough area for setting control?

If you could have enough area on UserForm to present all choice, you would set OptionButtons or CheckBoxes in Frame. If you could not have enough area, you could set ComboBox  or ListBox. Or you would have to adjust balance each other or expand UserForm area.

1.4 Is it possible that items may increase after system has been launched?

It’s a serious problem in management of database to force users to add items. It inserts items into transaction table, that isn’t exist in master table. It violates referential integrity constraints. I think that user should not be allowed to add items with ComboBox and new items should be added to master table on the other form.

Control Multiple choice One choose Area restriction Required item added
OptionButton   ✔    
CheckBox ✔      
ListBox ✔ ✔ ✔ ✔
ComboBox   ✔ ✔ ✔

2. TextBox

You can enter various data into TextBox, so it’s difficult control to master. It’s typical value list as below.

  • Last name and first name
  • Birthday
  • Gender
  • Organization, department
  • Zip code
  • Address
  • With or without of an attribute

These input values are classified as following data type:

2.1 String

Text data, for example, name of human, organization, department, zip code or address. Zip code should not be treated as numeric. Phone number should not be, so. Although these data have number, they should be treated as string and should be checked length of string or number of characters in validation.

2.2 Datetime

Date time data type, for example, birthday or entry date. Excel can treat date type after January 1, 1900. To tell the truth, Excel has bug in DATEDIFF function, it would not be so big problem for most purposes.

2.3 Numeric

Numeric required calculation such as finance or salary, measurement of experiment and physical quantity such as length or mass. For further classification, integer, decimal and currency. You would need to select appropriate decimal type depend on required accuracy.

2.4 Boolean

You would describe with boolean that you could tell with ‘yes’ or ‘no’, such as a disease status, smoking status or drinking status. But I think you should use Boolean not in TextBox but in CheckBox.

3. CommandButton

On CommandButton you could describe the procedure that is activated by click, such as selecting records from database, updating records in database, inserting records into database or deleting records from database.

  • Select record
  • Update record
  • Insert record
  • Validation
  • Delete record

3.1 Select record

To select and present records from database, you would need to specify search criteria. With such criteria as name, birthday, age or gender entered into TextBox or ListBox, searching with Auto Filter or Find method and presenting result records, you set the code on CommandButton to activate by click. ListBox might be most appropriate control, because obtained records would be more than one. It’s available to use whole match, forward match, backward match and intermediate match in search method, you could choose depend on situation. An error would occur if you couldn’t get records, so you should catch error and display alerts.

3.2 Update record

To update records in database, the data obtained by described as above have to be replicated to such controls that you can edit as TextBox, OptionButton or ListBox. You would set CommandButton to replicate data. You need to set CommandButton, code the procedure writing back the data you had fixed, that is activated by click.

3.3 Insert record

When there isn’t search result, it means that you should insert record into database. When you enter items into controls, system would be required to verify data. When entered data have passed validation, they would be allowed to be registered. If they didn’t pass validation, system should display alert to user.

3.4 Validation

There are formal and semantic validation. Formal validation verifies whether there is control without input, whether data type is appropriate. Semantic validation verifies that magnitude relation of number or context of date are appropriate. If incorrect data have been inserted into database, it’s hard to find it. It’s standard rule to validate data on user form. If you need, you could use regular expression. It’s one of the most important process in order to design robust system.

How to execute formal validation of TextBox on user form with EXCEL VBA?
How to validate empty value in controls on user form of Excel VBA?

3.5 Delete record

It may be required to remove record from database in some situation. When you operate worksheet as database, the record identified by Auto Filter or Find method should be removed by Delete method. “Delete” button should be set far from other buttons because of fail safe and when it’s clicked, system should ask user whether user really wishes to delete the record by message box.

4. Password

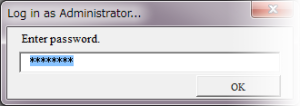
EnterPassword

It’s standard that system requires password when you open system as administrator. In order to enter password, you can use Input method or custom form. I’d like to recommend custom form.

Because Input method is easy to implement that Excel has already equipped function, you could trace user’s behavior with setting Variant type as return value. But it’s only and fatal defect that Input method couldn’t mask input value.

It’s true that custom form requires coding effort but it would be much more your benefit that you can mask password by modifying properties of TextBox.

How to validate password with regular expression which requires single-byte alphanumeric characters and symbols?

インターフェースとしてのEXCEL VBAによるユーザーフォーム

　Excel のユーザーフォームをデータベースのインターフェースとして使用する際の注意点などを述べます．ユーザーフォームにはデータを入力するためのコントロール，選択肢から選択させるためのコントロール，動作を記述するためのコントロールなどを配置します．それぞれの特徴を把握し，ユーザーにとって使いやすくかつ堅牢なシステムを構築する手助けとなれば幸いです．

  1. 選択肢としてのオプションボタン，チェックボックス，リストボックスおよびコンボボックス
  2. テキストボックス
  3. コマンドボタン
  4. パスワード入力

1. 選択肢としてのオプションボタン，チェックボックス，リストボックス及びコンボボックス

ExampleForm

1.1 コントロールを決める際の制約条件

　ユーザーフォーム上に選択肢を示す場合にどのコントロールを用いるかは状況に応じて決める必要があります．選択肢が一択なのか複数選択なのかが最も重要な制約条件です．次に選択肢を提示する面積が確保されているか否か，最後に選択肢をユーザー自身が追加する必要があるか否か，逆に言えば管理者が選択肢を定義しておく必要があるか否かでどのコントロールを用いるかが決まります．

1.2 選択肢は一択か複数か

　選択肢が一択である場合はオプションボタンをフレーム内に配置するか，コンボボックスを配置するかします．複数選択が必要であればチェックボックスをフレーム内に配置するか，リストボックスを配置するかします．ここで注意が必要ですが，複数選択を許可するということは値が一意に決まらないということであり，データベースのレコードを特定するためのキーの候補とはなり得ないということでもあります．もっと言えば，原子値ではなく配列ですので第一正規形を満たしません．EXCEL でそこまで考慮する必要があるかは分かりませんが，一応知っておく必要はあると思います．

1.3 配置するための面積は十分か

　選択肢を全て提示するのに必要な面積が十分に確保されていればフレーム内にオプションボタンを配置するか，チェックボックスを配置します．逆に面積が十分に確保できない場合はリストボックスまたはコンボボックスを配置します．複数選択が必要なのに十分な面積が確保できない場合は，他のコントロールとの配置のバランスを変更するか，ユーザーフォームの面積を拡張する必要があります．

1.4 選択項目は運用中に増加するか

　選択項目をユーザー自身に追加させる必要があるというのは，データベースの管理上問題があります．それはマスターテーブルにない項目をトランザクションテーブルに追加することに他ならず，参照整合性制約に違反します．少なくとも別のフォームでマスターテーブルに項目を追加する仕様とし，コンボボックスから新たに項目を追加するのを禁じた方がよいと思います．とはいえ実装ではなかなかそうも行かないのが現状です．

コントロール 複数選択 一択 面積に制約 アイテム追加必要
オプションボタン   ✔    
チェックボックス ✔      
リストボックス ✔ ✔ ✔ ✔
コンボボックス   ✔ ✔ ✔

ドロップダウンリストとコンボボックス

2. テキストボックス

　テキストボックスには様々なデータを入力できます．自由であるかゆえに最も扱いの難しいコントロールでもあります．考えられる入力値として代表的なものは以下の様なものではないでしょうか．

  • 人名
  • 生年月日
  • 性別
  • 組織名・部署名
  • 郵便番号
  • 住所
  • ある属性の有無

　これらの入力値はデータ型として以下のように分類できます．

2.1 文字列型

　人名，組織名・部署名，郵便番号，住所などのテキストデータ．郵便番号を数値型に含めるのは間違いです．先頭に 0 があった場合，数値型では削られてしまいます．同様に電話番号も数値型としてはいけません．これらは数値を使ってはいますが，文字列型として扱うべきであり，また文字数が決まっているため入力値のチェックの際には必ず文字数をチェックすべきです．

2.2 日付型

　生年月日や入社年月日などの日付のデータ．Excel では 1900 年 1 月 1 日以降の日付型を扱えます．DATEDIFF 関数などに多少のバグはあるのですが，通常の使用で問題になることはあまりないでしょう．

2.3 数値型

　数値型として扱うのは給与や財務など計算の必要なデータ，実験の測定値，長さや質量などの物理量などです．さらに細かく分類すると整数型や小数型，通貨型などいろいろあります．特に小数型は必要な精度に応じて適切なデータ型を選択する必要があります．

2.4 ブール型

　ある疾病の有無や既往の有無，喫煙や飲酒の有無など Yes か No で答えられるものについてはブール型で記述します．しかしブール型はテキストボックスよりもチェックボックスで使用した方が良いように思います．

3. コマンドボタン

　コマンドボタンにはクリックイベントにより意図する動作をプロシージャとして記述します．意図する動作とはデータベースからレコードを検索して表示すること，データベースに存在するレコードを修正すること，データベースにないレコードを新規に登録すること，データベースのレコードを削除することです．それぞれ SELECT, UPDATE, INSERT, DELETE に該当します．

  • レコードを検索する
  • レコードを修正する
  • レコードを登録する
  • 入力値のチェック
  • レコードを削除する

3.1 レコードを検索する

　データベースに存在するレコードを検索して表示するには検索条件を指定する必要があります．名前，生年月日，年齢，性別など検索に必要な条件をテキストボックスなりリストボックスなりに入力させ，オートフィルターや Find メソッドを使用して検索し，得られた結果を表示するコードを記述し，コマンドボタンのクリックイベントに登録します．結果を表示するコントロールはリストボックスが良いでしょう．おそらく複数の結果が得られる筈ですから．検索方法には全文一致，前方一致，後方一致，中間一致があり，状況に応じて選択します．結果が得られない場合はエラーが発生するため，エラーをキャッチして適切なアラートを表示させたほうが良いでしょう．

3.2 レコードを修正する

　データベースに存在するレコードを修正するには，前述の方法で得られたレコードをテキストボックスやオプションボタン，リストボックスなど編集可能なコントロールに移す必要があります．そのためのコマンドボタンを用意したほうが良いでしょう．必要な項目を訂正したらレコードをデータベースに書き戻す処理が必要になります．修正ボタンを配置し，コードを記述してクリックイベントに登録します．

3.3 レコードを登録する

　検索結果が存在しない場合とは，レコードを新規に登録する必要があるということです．ID, 名前など所定の項目をコントロールに入力させ，データベースに登録するコードを記述しますが，この際様々なチェックが必要になります．そのチェックに合格した場合にのみレコードを登録するコードを記述し，登録ボタンのクリックイベントに登録します．チェックに引っかかった部分をユーザーにフィードバックする機能があれば尚親切かもしれません．

3.4 入力値のチェック

　チェックの具体的な内容として，入力漏れがないか，適切なデータ型かなどの形式的なチェックと，さらに日付の前後関係や数値の大小関係といったセマンティックな要素も可能な限りチェックを行います．一旦誤ったデータがデータベースに登録されると簡単には見つけられません．ユーザーフォーム上で入力値のチェックを行うのが鉄則です．必要なら正規表現を使用して下さい．この部分の作り込みが使いやすいシステムになるか否かの分岐点になります．よく考えてコーディングして下さい．よくあるのが計算の必要な項目に全角数字を入力してしまったというものです．テキストボックスに半角数値のみの入力を受け付けるよう指定し，さらに入力モードを半角英数字に指定しておくなどの措置をプログラム上で行なっておけば済んだ話です．

Excel VBAでユーザーフォームのテキストボックスの値の形式的検証を行う
EXCEL VBA でユーザーフォーム上のコントロールの未入力を検証する

3.5 レコードを削除する

　データベースからレコードを削除する必要がある場合もあります．Excel のワークシートをデータベースにしている場合はフィルターを使ってレコードを指定し，Delete メソッドを使用して削除するコードをコマンドボタンに記述するのがよいでしょう．先述のレコードを検索して表示されたリストボックスから削除するレコードを選択させるのが安全な方法でしょう．削除ボタンは他のボタンと距離を離し，押し間違いを防ぐために一旦メッセージボックスで確認をとるなどの安全策を講じたほうが良いでしょう．

4. パスワード入力

EnterPassword

　メンテナンスのために管理者としてアプリケーションを開く必要がある場合，パスワードを要求するのが普通です．パスワードの入力には Input メソッドを使用する方法とパスワード入力用のユーザーフォームを自作する方法があります．それぞれメリットとデメリットがありますが，個人的には自作する方をお勧めします．

　Input メソッドは Excel で既に用意された機能ですので実装が容易です．戻り値に Variant 型を指定しておけばユーザーの行動を完全に把握出来ます．しかし唯一かつ致命的な欠点は入力値をマスクできないことです．この点で自作フォームをお勧めします．

　自作フォームではコーディングの手間がかかるデメリットがありますが，入力値をマスクできるメリットのほうが大きいと思います．ユーザーフォームにテキストボックスとコマンドボタンを配置し，テキストボックスのプロパティを設定するだけで入力値をマスク出来ます．

VBScriptの正規表現でパスワードに半角英数字と半角記号が使用されているか検証する

How to add direction into Excel custom lists?

When you’d like to sort with direction, you could not sort because Excel dose not have ‘Direction’ list. So in this article, I’d like to add ‘Direction’ into custom list. First, enter 16 direction from ‘North’ to ‘North-northwest’.

Custom list of direction
16 direction from North to North-northwest.

Next, select ‘File’ tab, ‘option’ and ‘Advanced settings’. After scroll down, press ‘Edit custom lists…’ button.

Edit custom list.
Edit custom list.

Click button on the right column of ‘Range of source list’.

Press button to select range.
Press button to select range.

Drag to select the range you entered ago, press button. Cell range would be entered into the column. Press ‘Import’ button.

Press "Import" button.
Press “Import” button.

OK, ‘Direction’ list has been added to custom lists. Press ‘OK’ to close window.

Custom list has been imported.
Custom list has been imported.

Excel2010のユーザー設定リストに方角を追加する

　Excel のソートの規定のリストには方角がありません．そこで方角のユーザー設定リストを追加します．新規にブックを開き，下図のように 16 の方角を入力しておきます．

Custom list of direction
16 direction from North to North-northwest.

　次に『ファイル』タブの『オプション』から『詳細設定』を選択します．スクロールしていくと下の方に『ユーザー設定リストの編集…』のボタンがあるのでクリックします．

Edit custom list.
Edit custom list.

　ユーザー設定リストパネルが開きます．『追加』ボタンを押して手入力することも可能ですが，先ほど入力しておいたリストを取り込むことにします．『リストの取込元範囲』にあるセル範囲指定ボタンをクリックします．

Press button to select range.
Press button to select range.

　先ほど入力したセル範囲をドラッグして選択し，ボタンをクリックすると『リストの取り込み範囲』にセル範囲が入力されます．『インポート』ボタンをクリックします．

Press "Import" button.
Press “Import” button.

　新たに方角リストが追加されました．『OK』をクリックして設定画面を抜けます．

Custom list has been imported.
Custom list has been imported.

Probability density function, expected value and variance of each probability distribution

I’d like to summarize probability density function (f(x)), expected value (E(X)) and variance (V(X)) of following probability distribution.

Supergeometric distribution  
\displaystyle f(x) = \frac{{}_{M}C_x\cdot{}_{N-M}C_{n-x}}{{}_{N}C_{n}} \displaystyle x = Max(0, n - (N - M)), \cdots, Min(n, M)
\displaystyle E(X) = np \displaystyle p = \frac{M}{N}
\displaystyle V(X) = np(1 - p)\frac{N - n}{N - 1}  
Binomial distribution  
\displaystyle f(x) = {}_{n}C_{x}p^{x}(1 - p)^{n - x} \displaystyle x = 0, 1, \cdots, n
\displaystyle E(X) = np \displaystyle 0 < p < 1[/latex]</td> </tr> <tr> <td>[latex]\displaystyle V(X) = np(1 - p)  
Poisson distribution  
\displaystyle f(x) = \frac{\exp(- \lambda)\cdot\lambda^x}{x!} \displaystyle x = 0, 1, 2, \cdots
\displaystyle E(X) = \lambda \lambda = np
\displaystyle V(X) = \lambda
Geometric distribution  
\displaystyle f(x) = p(1 - p)^{x - 1} \displaystyle x = 1, 2, 3, \cdots
\displaystyle E(X) = \frac{1}{p} \displaystyle 0 < p < 1[/latex]</td> </tr> <tr> <td>[latex]\displaystyle V(X) = \frac{1 - p}{p^2}  
Negative binomial distribution  
\displaystyle f(x) = {}_{k + x - 1}C_{x}p^{k}(1-p)^{x} \displaystyle x = 0, 1, 2, \cdots
\displaystyle E(X) = \frac{k(1 - p)}{p}  
\displaystyle V(X) = \frac{k(1 - p)}{p^2}  
Normal distribution  
\displaystyle f(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x - m)^2}{2\sigma^2}\right) \displaystyle - \infty < x < \infty[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = m  
\displaystyle V(X) = \sigma^2 \displaystyle \sigma > 0
Exponential distribution  
\displaystyle f(x) = \lambda\exp(-\lambda x) \displaystyle x \ge 0
\displaystyle f(x) = 0 \displaystyle x < 0[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = \frac{1}{\lambda}  
\displaystyle V(X) = \frac{1}{\lambda^2}  
Gamma distribution  
\displaystyle f(x) = \frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha - 1}\exp(- \lambda x) \displaystyle x \ge 0
\displaystyle f(x) = 0 \displaystyle x < 0[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = \frac{\alpha}{\lambda} \displaystyle \lambda, \alpha > 0
\displaystyle V(X) = \frac{\alpha}{\lambda^2}  
Beta distribution  
\displaystyle f(x) = \frac{x^{\alpha - 1}(1 - x)^{\beta - 1}}{B(\alpha, \beta)} \displaystyle 0 < x < 1[/latex]</td> </tr> <tr> <td>[latex]\displaystyle f(x) = 0 \displaystyle x \le 0, 1 \le x
\displaystyle E(X) = \frac{\alpha}{\alpha + \beta}  
\displaystyle V(X) = \frac{\alpha\beta}{(\alpha + \beta)^2(\alpha + \beta + 1)}  
Cauchy distribution  
\displaystyle f(x) = \frac{\alpha}{\pi(\alpha^2 + (x - \lambda)^2)} \displaystyle \alpha > 0
Log-normal distribution  
\displaystyle f(x) = \frac{1}{\sqrt{2\pi}\sigma x}\exp\left(-\frac{(\log(x) - m)^2}{2\sigma^2}\right) \displaystyle x > 0
\displaystyle f(x) = 0 \displaystyle x \le 0
\displaystyle E(X) = \exp\left(m + \frac{\sigma^2}{2}\right) \displaystyle \sigma > 0
\displaystyle V(X) = \exp[2m + \sigma^2](\exp[\sigma^2] - 1)  
Pareto distribution  
\displaystyle f(x) = \frac{x_0^\alpha}{x^{\alpha + 1}} \displaystyle x \ge x_0
\displaystyle f(x) = 0 \displaystyle x < 0[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = \frac{ax_0}{a - 1} \displaystyle a > 1
\displaystyle V(X) = \frac{ax_0^2}{a - 2} - \left(\frac{ax_0}{a - 1}\right)^2 \displaystyle a > 2
Weibull distribution  
\displaystyle f(x) = \frac{\gamma x^{\gamma - 1}}{\lambda^b}\exp\left[-\left(\frac{x}{y}\right)^\gamma\right] \displaystyle x \ge 0
\displaystyle f(x) = 0 \displaystyle x < 0[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = \lambda\Gamma\left(1 + \frac{1}{\gamma}\right) \displaystyle \lambda > 0
\displaystyle V(X) = \lambda^2\left[\Gamma\left(2 + \frac{1}{\gamma}\right) - \left(\Gamma\left(1 + \frac{1}{\gamma}\right)\right)^2\right] \displaystyle \gamma > 0

確率分布ごとの確率密度関数および期待値と分散

　確率分布ごとの確率密度関数 f(x), 確率変数 X の期待値 E(X) および分散 V(X) をまとめました．

超幾何分布  
\displaystyle f(x) = \frac{{}_{M}C_x\cdot{}_{N-M}C_{n-x}}{{}_{N}C_{n}} \displaystyle x = Max(0, n - (N - M)), \cdots, Min(n, M)
\displaystyle E(X) = np \displaystyle p = \frac{M}{N}
\displaystyle V(X) = np(1 - p)\frac{N - n}{N - 1}  
二項分布  
\displaystyle f(x) = {}_{n}C_{x}p^{x}(1 - p)^{n - x} \displaystyle x = 0, 1, \cdots, n
\displaystyle E(X) = np \displaystyle 0 < p < 1[/latex]</td> </tr> <tr> <td>[latex]\displaystyle V(X) = np(1 - p)  
ポアソン分布  
\displaystyle f(x) = \frac{\exp(- \lambda)\cdot\lambda^x}{x!} \displaystyle x = 0, 1, 2, \cdots
\displaystyle E(X) = \lambda \lambda = np
\displaystyle V(X) = \lambda
幾何分布  
\displaystyle f(x) = p(1 - p)^{x - 1} \displaystyle x = 1, 2, 3, \cdots
\displaystyle E(X) = \frac{1}{p} \displaystyle 0 < p < 1[/latex]</td> </tr> <tr> <td>[latex]\displaystyle V(X) = \frac{1 - p}{p^2}  
負の二項分布  
\displaystyle f(x) = {}_{k + x - 1}C_{x}p^{k}(1-p)^{x} \displaystyle x = 0, 1, 2, \cdots
\displaystyle E(X) = \frac{k(1 - p)}{p}  
\displaystyle V(X) = \frac{k(1 - p)}{p^2}  
正規分布  
\displaystyle f(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x - m)^2}{2\sigma^2}\right) \displaystyle - \infty < x < \infty[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = m  
\displaystyle V(X) = \sigma^2 \displaystyle \sigma > 0
指数分布  
\displaystyle f(x) = \lambda\exp(-\lambda x) \displaystyle x \ge 0
\displaystyle f(x) = 0 \displaystyle x < 0[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = \frac{1}{\lambda}  
\displaystyle V(X) = \frac{1}{\lambda^2}  
ガンマ分布  
\displaystyle f(x) = \frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha - 1}\exp(- \lambda x) \displaystyle x \ge 0
\displaystyle f(x) = 0 \displaystyle x < 0[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = \frac{\alpha}{\lambda} \displaystyle \lambda, \alpha > 0
\displaystyle V(X) = \frac{\alpha}{\lambda^2}  
ベータ分布  
\displaystyle f(x) = \frac{x^{\alpha - 1}(1 - x)^{\beta - 1}}{B(\alpha, \beta)} \displaystyle 0 < x < 1[/latex]</td> </tr> <tr> <td>[latex]\displaystyle f(x) = 0 \displaystyle x \le 0, 1 \le x
\displaystyle E(X) = \frac{\alpha}{\alpha + \beta}  
\displaystyle V(X) = \frac{\alpha\beta}{(\alpha + \beta)^2(\alpha + \beta + 1)}  
コーシー分布  
\displaystyle f(x) = \frac{\alpha}{\pi(\alpha^2 + (x - \lambda)^2)} \displaystyle \alpha > 0
対数正規分布  
\displaystyle f(x) = \frac{1}{\sqrt{2\pi}\sigma x}\exp\left(-\frac{(\log(x) - m)^2}{2\sigma^2}\right) \displaystyle x > 0
\displaystyle f(x) = 0 \displaystyle x \le 0
\displaystyle E(X) = \exp\left(m + \frac{\sigma^2}{2}\right) \displaystyle \sigma > 0
\displaystyle V(X) = \exp[2m + \sigma^2](\exp[\sigma^2] - 1)  
パレート分布  
\displaystyle f(x) = \frac{x_0^\alpha}{x^{\alpha + 1}} \displaystyle x \ge x_0
\displaystyle f(x) = 0 \displaystyle x < 0[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = \frac{ax_0}{a - 1} \displaystyle a > 1
\displaystyle V(X) = \frac{ax_0^2}{a - 2} - \left(\frac{ax_0}{a - 1}\right)^2 \displaystyle a > 2
ワイブル分布  
\displaystyle f(x) = \frac{\gamma x^{\gamma - 1}}{\lambda^b}\exp\left[-\left(\frac{x}{y}\right)^\gamma\right] \displaystyle x \ge 0
\displaystyle f(x) = 0 \displaystyle x < 0[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = \lambda\Gamma\left(1 + \frac{1}{\gamma}\right) \displaystyle \lambda > 0
\displaystyle V(X) = \lambda^2\left[\Gamma\left(2 + \frac{1}{\gamma}\right) - \left(\Gamma\left(1 + \frac{1}{\gamma}\right)\right)^2\right] \displaystyle \gamma > 0

How to calculate required sample size in chi-square test, Fisher exact test, Student’s t-test and log-rank test?

Sample size calculation may be hard for research member, because it’s difficult to distinguish sample size is enough or not when it was not statistical significant. Required sample size calculation is very important.

χ2 test without correction

To compare survival rate between risk/intervention group and control group, it’s required to execute χ2 test. You can calculate sample size as following formula. With significance level (α) 0.05 (two-tailed) and statistical power (1 – β) 0.8 (one-sided), Zα/2 is 1.96 and Zβ is 0.84, respectively.

\displaystyle N_0 = \frac{\left(Z_{\alpha/2}\sqrt{(1+\phi)\bar{p}(1 - \bar{p})} + Z_\beta\sqrt{\phi p_0(1 - p_0) + p_1(1 - p_1)}\right)^2}{\phi\delta^2}

\displaystyle N_1 = \phi N_0

If effect size δ was expressed with odd ratio (OR), sample size could be calculated as formula below.

\displaystyle N_0 = \left(\frac{1 + \phi}{\phi}\right)\frac{(Z_{\alpha/2} + Z_\beta)^2}{(\log{OR})^2\bar{p}(1 - \bar{p})}

\displaystyle N_1 = \phi N_0

\displaystyle N_0 : required number of control group.

\displaystyle N_1 : required number of risk/intervention group.

\displaystyle n_0 : actual number of control group.

\displaystyle n_1 : actual number of risk/intervention group.

\displaystyle \phi = \frac{n_1}{n_0}: the ratio of number of risk/intervention group to number of control group.

\displaystyle p_0 : survival rate or efficacy in control group.

\displaystyle p_1 : survival rate or efficacy in risk/intervention group.

\displaystyle \delta = p_1 - p_0 : effect size, difference between two groups.

\displaystyle \bar{p} = \frac{p_0 + \phi p_1}{1 + \phi}

χ2 test with Yates correction and Fisher exact test

When you execute χ2 test with Yates correction or Fisher exact test, you have to correct N0 with multiplying by C, correction term as below.

\displaystyle C = \frac{1}{4}\left(1 + \sqrt{1 + \frac{2 (1 + \phi)}{\phi N_0 |\delta|}}\right)^2

Student’s t-test

In Student’s t-test, you have to calculate standardized effect size (Δ) first with a mean of control group and a mean of risk/intervention group. Then you can calculate sample size with Δ as below. It’s assumed that the variances are equal between control group and risk/intervention group.

\displaystyle \Delta = \frac{|\mu_0 - \mu_1|}{\sigma}

\displaystyle N_0 = \left(\frac{1 + \phi}{\phi}\right)\frac{(Z_{\alpha/2} + Z_{\beta})^2}{\Delta^2} + \frac{Z_{\alpha/2}^2}{2(1 + \phi)}

\displaystyle N_1 = \phi N_0

log-rank test

In log-rank test, you can calculate required number of event (e) and sample size (N) as following formula. p0 and p1 are cumulative survival rate of control group and risk/intervention group, respectively, derived from previous research or cumulative survival rate after 1 or 2 years from the research started. When φ was 1, it means equal sample size in both groups, it would bring same result as described in How to calculate appropriate sample size in Cox proportional hazard analysis with cross tabulation?.

\displaystyle \theta = \frac{\log(p_1)}{\log(p_0)}

\displaystyle e_0 = \frac{1}{(1 + \phi)\phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2(Z_{\alpha/2} + Z_\beta)^2

\displaystyle e_1 = \phi e_0 = \frac{1}{1 + \phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2(Z_{\alpha/2} + Z_\beta)^2

\displaystyle e = e_0 + e_1 = \frac{1}{\phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2(Z_{\alpha/2} + Z_\beta)^2

\displaystyle N_0 = \frac{e}{(1 - p_0) + \phi(1 - p_1)} = \frac{1}{\phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2\frac{(Z_{\alpha/2} + Z_\beta)^2}{(1 - p_0) + \phi(1 - p_1)}

\displaystyle N_1 = \phi N_0

\displaystyle N = N_0 + N_1 = \frac{1 + \phi}{\phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2\frac{(Z_{\alpha/2} + Z_\beta)^2}{(1 - p_0) + \phi(1 - p_1)}

\displaystyle N_0 : required number of control group.

\displaystyle N_1 : required number of risk/intervention group.

\displaystyle n_0 : actual number of control group.

\displaystyle n_1 : actual number of risk/intervention group.

\displaystyle \phi = \frac{n_1}{n_0} : the ratio of number of risk/intervention group to number of control group.

\displaystyle p_0 : survival rate or efficacy of control group.

\displaystyle p_1 : survival rate or efficacy of risk/intervention group.

References:
TABLES OF THE NUMBER OF PATIENTS REQUIRED IN CLINICAL TRIALS USING THE LOG RANK TEST

χ2乗検定，Fisher正確確率検定，Student t検定およびlog-rank検定においてサンプルサイズを計算するには

　サンプルサイズの計算は重要です．多くの研究者にとって統計的有意差が出なかった場合に，それがサンプルサイズ不足が原因によるものかどうかの判断ができないからです．全ての検定を網羅することはできませんでしたが，重要と思われる主な検定においてサンプルサイズを計算する方法を述べます．

χ2検定

　リスク群・介入群と対照群との2群間で有効率・生存率を比較するにはχ2乗検定を行いますが，その際のサンプルサイズの算出には下記の式を用います．α = 0.05 （両側）, 1 – β = 0.8 （片側）とすると Zα/2 = 1.96, Zβ = 0.84 として計算します．

\displaystyle N_0 = \frac{\left(Z_{\alpha/2}\sqrt{(1+\phi)\bar{p}(1 - \bar{p})} + Z_\beta\sqrt{\phi p_0(1 - p_0) + p_1(1 - p_1)}\right)^2}{\phi\delta^2}

\displaystyle N_1 = \phi N_0

　効果量 δ がオッズ比で表現できる場合，サンプルサイズは下式で求まります．

\displaystyle N_0 = \left(\frac{1 + \phi}{\phi}\right)\frac{(Z_{\alpha/2} + Z_\beta)^2}{(\log{OR})^2\bar{p}(1 - \bar{p})}

\displaystyle N_1 = \phi N_0

\displaystyle N_0 : 対照群に必要なサンプルサイズ

\displaystyle N_1 : リスク群・介入群に必要なサンプルサイズ

\displaystyle n_0 : 対照群の実際の症例数

\displaystyle n_1 : リスク群・介入群の実際の症例数

\displaystyle \phi = \frac{n_1}{n_0}

\displaystyle p_0 : 対照群の有効率・生存率

\displaystyle p_1 : リスク群・介入群の有効率・生存率

\displaystyle \delta = p_1 - p_0 : リスク群・介入群と対照群との有効率・生存率の差

\displaystyle \bar{p} = \frac{p_0 + \phi p_1}{1 + \phi}

Yates補正による χ2 検定と Fisher 正確確率検定

　Yates 補正や Fisher 正確確率検定の際には N0 に補正項 C を乗じて補正する必要があります．リンクした書籍には平方根内の項に 1 を加算していますが，森實敏夫の教科書には加算していません．しかしウェブ上のサンプルサイズの計算の数式は合っています．

\displaystyle C = \frac{1}{4}\left(1 + \sqrt{1 + \frac{2 (1 + \phi)}{\phi N_0 |\delta|}}\right)^2

Student t 検定

　対照群の平均値 μ0 およびリスク群・介入群の平均値 μ1 から効果量 Δ を計算し，そこからサンプルサイズを求めます．この場合，対照群とリスク群・介入群とでは分散が等しいと仮定しています．

\displaystyle \Delta = \frac{|\mu_0 - \mu_1|}{\sigma}

\displaystyle N_0 = \left(\frac{1 + \phi}{\phi}\right)\frac{(Z_{\alpha/2} + Z_{\beta})^2}{\Delta^2} + \frac{Z_{\alpha/2}^2}{2(1 + \phi)}

\displaystyle N_1 = \phi N_0

log-rank 検定

　log-rank 検定において必要なイベント数 e およびサンプルサイズ N は Freedman の方法で下式にて求まります．p0 および p1 は先行研究や試験開始後 1－2 年での累積生存率です．φ = 1 の場合，COX比例ハザードモデルのlog-rank検定に必要なサンプルサイズを四分表から計算するで説明した数式と同じ結果になります．

　森實敏夫の教科書の記載には誤りがあります．イベント数 e を求める式の分母において，Freedman の原著では φ は括弧の外にありますが，森實敏夫の教科書の記載では括弧内にあります．ウェブ上のサンプルサイズの計算の数式は合っています．参考文献の Freedman の原著は有料です．

\displaystyle \theta = \frac{\log(p_1)}{\log(p_0)}

\displaystyle e_0 = \frac{1}{(1 + \phi)\phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2(Z_{\alpha/2} + Z_\beta)^2

\displaystyle e_1 = \phi e_0 = \frac{1}{1 + \phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2(Z_{\alpha/2} + Z_\beta)^2

\displaystyle e = e_0 + e_1 = \frac{1}{\phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2(Z_{\alpha/2} + Z_\beta)^2

\displaystyle N_0 = \frac{e}{(1 - p_0) + \phi(1 - p_1)} = \frac{1}{\phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2\frac{(Z_{\alpha/2} + Z_\beta)^2}{(1 - p_0) + \phi(1 - p_1)}

\displaystyle N_1 = \phi N_0

\displaystyle N = N_0 + N_1 = \frac{1 + \phi}{\phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2\frac{(Z_{\alpha/2} + Z_\beta)^2}{(1 - p_0) + \phi(1 - p_1)}

\displaystyle N_0 : 対照群に必要なサンプルサイズ

\displaystyle N_1 : リスク群・介入群に必要なサンプルサイズ

\displaystyle n_0 : 対照群の実際の症例数

\displaystyle n_1 : リスク群・介入群の実際の症例数

\displaystyle \phi = \frac{n_1}{n_0} : リスク群・介入群の症例数と対照群の症例数との比

\displaystyle p_0 : 対照群の有効率・生存率

\displaystyle p_1 : リスク群・介入群の有効率・生存率

参考文献：
TABLES OF THE NUMBER OF PATIENTS REQUIRED IN CLINICAL TRIALS USING THE LOG RANK TEST

Primary Prevention of Cardiovascular Disease with a Mediterranean Diet

Outcome of PREDIMED Study has been published in the New England Journal of Medicine that examined primary prevention of cardiovascular disease with Mediterranean diet. The result has been shown that Mediterranean diet with extra-virgin olive oil or mixed nuts has better prognosis than reduction of lipid. It is considered that alpha linolenic acid rich Mediterranean diet, a component of walnuts, influences oxidative stress, inflammation or endothelial dysfunction.

Primary Prevention of Cardiovascular Disease with a Mediterranean Diet

Ramón Estruch, M.D., Ph.D., Emilio Ros, M.D., Ph.D., Jordi Salas-Salvadó, M.D., Ph.D., Maria-Isabel Covas, D.Pharm., Ph.D., Dolores Corella, D.Pharm., Ph.D., Fernando Arós, M.D., Ph.D., Enrique Gómez-Gracia, M.D., Ph.D., Valentina Ruiz-Gutiérrez, Ph.D., Miquel Fiol, M.D., Ph.D., José Lapetra, M.D., Ph.D., Rosa Maria Lamuela-Raventos, D.Pharm., Ph.D., Lluís Serra-Majem, M.D., Ph.D., Xavier Pintó, M.D., Ph.D., Josep Basora, M.D., Ph.D., Miguel Angel Muñoz, M.D., Ph.D., José V. Sorlí, M.D., Ph.D., José Alfredo Martínez, D.Pharm, M.D., Ph.D., and Miguel Angel Martínez-González, M.D., Ph.D., for the PREDIMED Study Investigators

N Engl J Med 2013;368:1279-90

Background

Observational cohort studies and a secondary prevention trial have shown an inverse association between adherence to the Mediterranean diet and cardiovascular risk. We conducted a randomized trial of this diet pattern for the primary prevention of cardiovascular events.

Methods

In a multicenter trial in Spain, we randomly assigned participants who were at high cardiovascular risk, but with no cardiovascular disease at enrollment, to one of three diets: a Mediterranean diet supplemented with extra-virgin olive oil, a Mediterranean diet supplemented with mixed nuts, or a control diet (advice to reduce dietary fat). Participants received quarterly individual and group educational sessions and, depending on group assignment, free provision of extra-virgin olive oil, mixed nuts, or small nonfood gifts. The primary end point was the rate of major cardiovascular events (myocardial infarction, stroke, or death from cardiovascular causes). On the basis of the results of an interim analysis, the trial was stopped after a median follow-up of 4.8 years.

Results

A total of 7447 persons were enrolled (age range, 55 to 80 years); 57% were women. The two Mediterranean-diet groups had good adherence to the intervention, according to self-reported intake and biomarker analyses. A primary end-point event occurred in 288 participants. The multivariable-adjusted hazard ratios were 0.70 (95% confidence interval [CI], 0.54 to 0.92) and 0.72 (95% CI, 0.54 to 0.96) for the group assigned to a Mediterranean diet with extra-virgin olive oil (96 events) and the group assigned to a Mediterranean diet with nuts (83 events), respectively, versus the control group (109 events). No diet-related adverse effects were reported.

Conclusions

Among persons at high cardiovascular risk, a Mediterranean diet supplemented with extra-virgin olive oil or nuts reduced the incidence of major cardiovascular events.

References:
Effects of a Mediterranean-Style Diet on Cardiovascular Risk Factors
Effect of a Mediterranean-Style Diet on Endothelial Dysfunction and Markers of Vascular Inflammation in the Metabolic Syndrome
Mediterranean-style diet and risk of ischemic stroke, myocardial infarction, and vascular death: the Northern Manhattan Study

地中海食による心血管疾患の一次予防

　地中海食による心血管疾患の予防効果を検討した PREDIMED Study の成果が New England Journal に掲載されました．単に脂質を制限するよりもオリーブオイルやナッツを摂取したほうが心血管疾患の一次予防に有効であったとする結果です．地中海食には胡桃の成分であるαリノレン酸が豊富に含まれており，酸化ストレスや炎症，内皮機能障害などに影響するからではないかと考察しています．



地中海食による心血管疾患の一次予防

Ramón Estruch, M.D., Ph.D., Emilio Ros, M.D., Ph.D., Jordi Salas-Salvadó, M.D., Ph.D., Maria-Isabel Covas, D.Pharm., Ph.D., Dolores Corella, D.Pharm., Ph.D., Fernando Arós, M.D., Ph.D., Enrique Gómez-Gracia, M.D., Ph.D., Valentina Ruiz-Gutiérrez, Ph.D., Miquel Fiol, M.D., Ph.D., José Lapetra, M.D., Ph.D., Rosa Maria Lamuela-Raventos, D.Pharm., Ph.D., Lluís Serra-Majem, M.D., Ph.D., Xavier Pintó, M.D., Ph.D., Josep Basora, M.D., Ph.D., Miguel Angel Muñoz, M.D., Ph.D., José V. Sorlí, M.D., Ph.D., José Alfredo Martínez, D.Pharm, M.D., Ph.D., and Miguel Angel Martínez-González, M.D., Ph.D., for the PREDIMED Study Investigators

N Engl J Med 2013; 368:1279-1290

要旨

背景

　観察コホート研究と二次予防試験は，地中海食の順守と心血管リスクとの間の逆相関を示した．我々は心血管疾患の一次予防のためこの食事様式の無作為化試験を実施した．

方法

　スペインにおける多施設で我々は心血管疾患リスクが高いが心血管疾患に罹患していない参加者を３つの食事群の一つに無作為割り付けした．エクストラバージンオリーブオイルを提供される地中海食群，ミックスナッツを低供される地中海食群，対照群で食事脂質を減量するよう指導された群である．参加者は四半期ごとに個別またはグループで教育セッションを受け，割り付けに従って無料でエクストラバージンオリーブオイルか，ミックスナッツか，少量の食品でない贈呈品を受け取った．一次エンドポイントは主要な心血管イベント（心筋梗塞，脳卒中または心血管由来の死亡）の率とした．暫定的な解析に基づいて，試験は経過観察期間の中央値が4.8年となった後に中止した．

結果

　全体で 7447 名（55 歳から 80 歳まで）の参加者が登録され，うち 57 % が女性であった．自己申告による摂食調査と生化学検査によると，地中海食の2群では介入に対して良好な順守が得られた．288 名において一次エンドポイント事象が発生した．エクストラバージンオリーブオイルを提供された地中海食群（96件）およびミックスナッツを提供された地中海食群（83件）の対照群（109件）に対する多変量調整したハザード比はそれぞれ 0.70 (95%CI 0.54 – 0.92) および 0.72 (95%CI 0.54 – 0.96) であった．食事に関連する副作用は全く認めなかった．

結論

　心血管リスクの高い人にとって，エクストラバージンオリーブオイルまたはミックスナッツを提供された地中海食は心血管イベントの発生を減少させた．

参照：
心血管危険因子における地中海料理の効果
メタボリック症候群における内皮機能障害と血管炎症マーカーに対する地中海式料理の影響
地中海式料理と虚血性脳卒中，心筋梗塞，血管死との関連：the Northern Manhattan Study

How to calculate appropriate sample size in Cox proportional hazard analysis with cross tabulation?

In this article, I’d like to describe how to calculate appropriate sample size in Cox proportional analysis with cross tabulation, a error and b error. a error is called as statistical significance or type 1 error and b error is called as type 2 error, respectively. 1 – b is called as statistical power. a is usually configured at 0.05 (two-tailed) and b is configured at 0.2 (one-sided), respectively. As a result, Za/2 is 1.96 and Zb is 0.84, respectively.

I’d like to assume that S1 is survival rate of risk group or intervention group and S0 is survival rate of control group, without risk or intervention. q is ratio of logarithm of them.

\displaystyle LN(S_1) = Exp(B)LN(S_0)\vspace{0.1in}\\\theta = Exp(B) = \frac{LN(S_1)}{LN(S_0)}

I’d like to use cross tabulation here. You can replace endpoint with death or failure.

ENDPOINT CENSOR Marginal total
POSITIVE a b a + b
NEGATIVE c d c + d
Marginal total a + c b + d N
\displaystyle S_1 = \frac{b}{a+b}\vspace{0.1in}\\S_0 = \frac{d}{c+d}

You can calculate estimated number of death (e) in both group as following formula by Freedman’s approximate calculation.

\displaystyle e = \left(\frac{\theta+1}{\theta-1}\right)^2(Z_{\alpha/2}+Z_\beta)^2

You can calculate entry size (n) in each group, as following formula.

\displaystyle e = n(1-S_0)+n(1-S_1)\vspace{0.1in}\\n = \frac{e}{2 - S_0 - S_1}

You have to correct entry size with drop-out rate (w) as following formula. Throughout trial, two times of n is needed.

\displaystyle n = \frac{e}{(2 - S_0 - S_1)(1-w)}

COX比例ハザードモデルのlog-rank検定に必要なサンプルサイズを四分表から計算する

　COX 比例ハザード解析はリスクの有無や治療介入の有無に対して，生存率や故障率の違いの差を検定する方法です．最終的には四分表に集約可能ですが，解析手段として試験期間にエントリーした症例を，エンドポイント発生までの生存期間を昇順でソートして，エンドポイントが発生するたびに累積生存率を再計算します．

　今回は四分表から計算した生存率の差，aエラー，bエラーから必要なサンプルサイズを計算します．aエラーとは有意確率または第1種の過誤といい，bエラーとは第2種の過誤ともいいます．1 – b のことを検出力といいます．通常ですとa = 0.05（両側），1 – b = 0.8（片側）とすることが多く，その場合 Za/2 = 1.96, Zb = 0.84 とします．当然ながら，リスク群と対照群との生存率の差が小さいほど必要なサンプルサイズは増えます．

　S1 はリスク群や介入群の生存率，S0 はリスクなし，介入なしなどいわゆる対照群の生存率とします．q はそれらの対数の比で，追跡終了時点での生存率の比です．

\displaystyle LN(S_1) = Exp(B)LN(S_0)\vspace{0.1in}\\\theta = Exp(B) = \frac{LN(S_1)}{LN(S_0)}

　ここで再び四分表が登場します．エンドポイントと打ち切りはそれぞれ死亡と打ち切り，故障と打ち切りなどと読み替え可能です．

  ENDPOINT CENSOR Marginal total
POSITIVE a b a + b
NEGATIVE c d c + d
Marginal total a + c b + d N

\displaystyle S_1 = \frac{b}{a+b} \displaystyle S_0 = \frac{d}{c+d}

　とすると Freedman による近似計算として両群での期待死亡値 e は下記の式で表現出来ます．

\displaystyle e = \left(\frac{\theta+1}{\theta-1}\right)^2(Z_{\alpha/2}+Z_\beta)^2

　n を各群で必要なエントリーサイズとして e をリスク群と対照群の死亡率で割り付けると下記の式で表現出来ます．

\displaystyle e = n(1-S_0)+n(1-S_1)

　これを n について解くと下記の式となります．

\displaystyle n = \frac{e}{2 - S_0 - S_1}

　脱落率を w とすると補正式は下記のとおりです．試験全体では 2n のサンプルサイズが必要です．

\displaystyle n = \frac{e}{(2 - S_0 - S_1)(1-w)}

Geriatric Nutritional Risk Index, a simplified nutritional screening index, is a significant predictor of mortality in chronic dialysis patients

Zadeh has reported that malnutrition-Inflammation Score (MIS) is predictor of mortality in hemodialysis patients. Although Yamada has reported that the significant correlation between Geriatric Nutritional Risk Index (GNRI) and MIS, they did not report the correlation between GNRI and mortality in chronic hemodialysis patients. This article has reported that GNRI is significant predictor of mortality in chronic dialysis patients.

Geriatric Nutritional Risk Index, a simplified nutritional screening index, is a significant predictor of mortality in chronic dialysis patients

Ikue Kobayashi, Eiji Ishimura, Yoko Kato, Senji Okuno, Tadashi Yamamoto, Tomoyuki Yamakawa, Katsuhito Mori, Masaaki Inaba and Yoshiki Nishizawa

Nephrol Dial Transplant (2010) 25: 3361-3365

Abstract

Background

Malnutrition is a common complication in haemodialysis patients. Recently, the Geriatric Nutritional Risk Index (GNRI) has been reported as a simple and accurate tool to assess nutritional status of haemodialysis patients. Our objective was to examine the association between GNRI and mortality in chronic haemodialysis patients.

Methods

We examined the GNRI of 490 maintenance haemodialysis patients (60 ± 12 years, 293 males and 197 females) and followed up these patients for 60 months. Predictors for all-cause death were examined using Kaplan–Meier analysis and Cox proportional analyses.

Results

The GNRI was 98.0 ± 6.0, and was significantly and negatively correlated with age and haemodialysis duration. During the 60-month follow-up period, 129 patients died. According to the highest positive likelihood and risk ratios, the cutoff value of GNRI for mortality was set at 90. Kaplan–Meier analysis revealed that patients with a GNRI <90 (n = 50) had a significantly lower survival rate, compared to those with GNRI ≥90 (n = 440) (log-rank test, P < 0.0001). Multivariate Cox proportional hazards analyses demonstrated that GNRI was a significant predictor for mortality [hazard ratio (HR) 0.962, 95% confidence interval (CI) 0.931–0.995, P < 0.05], after adjustment for age, gender, C-reactive protein, presence of diabetes and haemodialysis duration.

Conclusions

These results demonstrated that GNRI is a significant predictor for mortality in haemodialysis patients. The simple method of GNRI is considered to be a clinically useful marker for the assessment of nutritional status in haemodialysis patients.

Keywords: Geriatric Nutritional Risk Index; haemodialysis; malnutrition; mortality