Partial derivatives | Improve Society

The partial derivatives of $f(x, y)$ with respect to x and y are defined by
$\displaystyle \frac{\partial f}{\partial x}= \lim\limits_{h \rightarrow 0} \frac{f(x + h, y) - f(x, y)}{h}\\\vspace{0.2 in} \frac{\partial f}{\partial y} = \lim\limits_{k \rightarrow 0} \frac{f(x, y + k) - f(x, y)}{k}$
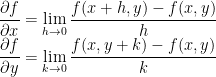
if these limits exist. It’s often written h = Δx, k = Δy. Note that $\partial f/\partial x$ is simply the ordinary derivative of f with respect to x keeping y constant, while $\partial f/\partial y$ is the ordinary derivative of f with respect to y keeping x constant.

Higher derivatives are defined similarly. For example, you have the second order derivatives
$\displaystyle \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial^2f}{\partial x^2}\\\vspace{0.2 in} \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right) = \frac{\partial^2f}{\partial x\partial y}\\\vspace{0.2 in} \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial^2f}{\partial y\partial x}\\\vspace{0.2 in} \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right) = \frac{\partial^2f}{\partial y^2}$
The deviation are sometimes denoted f_x and f_y. In such case f_x(a, b), f_y(a, b) denote these partial derivatives evaluated at (a, b).

The deviations are denoted by f_xx, f_xy, f_yx, f_yy respectively. The second and third results will be the same if f has continuous partial derivatives of second order at least.

The differentiation of f(x, y) is defined as
$\displaystyle df = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy$
where h = Δx = dx, k = Δy = dy.