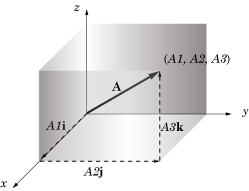
Components of a vector | Improve Society

Any vector $\bold{A}$ in 3 dimensions can be represented with initial point at the origin O of a rectangular coordinate system. Let $(A_1, A_2, A_3)$ be the rectangular coordinates of the terminal point of vector $\bold{A}$ with initial point at O. The vectors $A_1\bold{i}$ , $A_2\bold{j}$ and $A_3\bold{k}$ are called the rectangular component vectors, or simply component vectors, of $\bold{A}$ in the x, y and z directions respectively. $A_1$ , $A_2$ and $A_3$ are called the rectangular components, or simply components, of $\bold{A}$ in the x, y and z directions respectively.

The sum or resultant of $A_1\bold{i}$ , $A_2\bold{j}$ and $A_3\bold{k}$ is the vector $\bold{A}$ , so that we can write
$\bold{A} = A_1\bold{i} + A_2\bold{j} + A_3\bold{k}\cdots(1)$
The magnitude of $\bold{A}$ is
$A = |\bold{A}| = \sqrt{A_1^2 + A_2^2 + A_3^2}\cdots(2)$
In particular, the position vector or radius vector $\bold{r}$ from O to the point (x, y, z) is written
$\bold{r} = x\bold{i} + y\bold{j} + z\bold{k}\cdots(3)$
and has magnitude $r = |\bold{r}| = \sqrt{x^2 + y^2 + z^2}$ .