ベクトルの成分

このエントリーをはてなブックマークに追加
Pocket

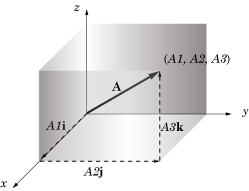
　3次元におけるいかなるベクトル \bold{A} も直交座標系の原点 O における始点により表現可能です．ここでベクトル \bold{A} を直交座標系における原点 O を始点とし (A_1, A_2, A_3) を終点としましょう．そのベクトル A_1\bold{i}, A_2\bold{j} および A_3\bold{k} はそれぞれ \bold{A} における x, y および z 軸方向の 直交成分ベクトル, あるいは単に 成分ベクトル といいます．A_1, A_2 および A_3 はそれぞれ x, y および z 軸方向における \bold{A} の 直交成分, または単に 成分 と呼ばれます．

　A_1\bold{i}, A_2\bold{j} および A_3\bold{k} の和や結果が \bold{A} であり，ゆえに

\bold{A} = A_1\bold{i} + A_2\bold{j} + A_3\bold{k}\cdots(1)

　\bold{A} の大きさは

A = |\bold{A}| = \sqrt{A_1^2 + A_2^2 + A_3^2}\cdots(2)

　特に，原点 O から点 (x, y, z) への 位置ベクトル または 動径ベクトル \bold{r} は以下のように記述できます．

\bold{r} = x\bold{i} + y\bold{j} + z\bold{k}\cdots(3)

またその大きさは r = |\bold{r}| = \sqrt{x^2 + y^2 + z^2} となります．

Vector

このエントリーをはてなブックマークに追加
Pocket

投稿者: admin

趣味：写真撮影とデータベース． カメラ：TOYO FIELD, Hasselblad 500C/M, Leica M6． SQL Server 2008 R2, MySQL, Microsoft Access．

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です