線積分 | Improve Society

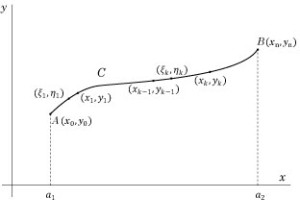
　C を xy 平面において 2 点 $A (a_1, b_1)$ および $B (a_2, b_2)$ をつなぐ曲線とします（Fig. 6-2参照）． $P(x, y)$ および $Q(x, y)$ を曲線 C 上のすべての点を定義する単一値関数とします． $(x_1, y_1),\ (x_2, y_2),\ \dots,\ (x_{n-1}, y_{n-1})$ により得られた n – 1 個の点を選択して C を n 個に細分化します．Call $\Delta x_k = x_k - x_{k-1}$ および $\Delta y_k = y_k - y_{k-1},\ k = 1,\ 2,\ \dots\ n$ を呼び，C 上にあり点 $(x_{k-1}, y_{k-1})$ および点 $(x_k, y_k)$ の間にあるような点 $(\xi_k, \eta_k)$ を想定します．以下のように和を形成します．

$\displaystyle \sum_{k=1}^{n}\{P(\xi_k, \eta_k)\Delta x_k + Q(\xi_k, \eta_k)\Delta y_k\}\cdots(13)$

　仮に極限が存在するなら $n\rightarrow\infty$ となるにつれ全ての $\Delta x_k,\ \Delta y$ の量はゼロに近づき，この和の極限を C 周りの 線積分 と呼び，以下のように記述します．

$\displaystyle \int_C \left[ P(x, y)dx + Q(x, y)dy \right]$ または $\displaystyle \int_{(a_1, b_1)}^{(a_2, b_2)}\left[ Pdx + Qdy \right]\cdots(14)$

　P および Q が C 上の全ての点について連続（または区間的に連続）ならこの極限は存在します．その積分値は一般に P, Q, 特に曲線 C に依存し，また $(a_1, b_1)$ および $(a_2, b_2)$ の極限に依存します．

　正確に類似した方法で 3 次元空間における曲線 C 周りの線積分を以下のように定義できるでしょう．

$\displaystyle \lim\limits_{n \rightarrow\infty}\sum_{k=1}^{n}\left\{ A_1(\xi_k, \eta_k, \zeta_k)\Delta x_k + A_2(\xi_k, \eta_k, \zeta_k)\Delta y_k + A_3(\xi_k, \eta_k, \zeta_k)\Delta z_k \right\} \\ = \int_C \left[ A_1dx + A_2dy + A_3dz \right] \cdots(15)$

ここで $A_1$ , $A_2$ および $A_3$ は $x$ , $y$ および $z$ の関数です．