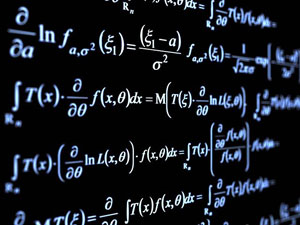STOKE'S THEOREM | Improve Society

Let $S$ be an open, two-sided surface bounded by a closed non-intersecting curve $C$ (simple closed curve). Consider a directed line normal to $S$ as positive if it is on one side of $S$ , and negative if it is on the other side of $S$ . The choice of which side is positive is arbitrary but should be decided upon in advance. Call the direction or sense of $C$ positive if an observer, walking on the boundary of $S$ with his head pointing in the direction of the positive normal, has the surface on his left. Then if $A_1,\ A_2,\ A_3$ are single-valued, continuous, and have continuous first partial derivatives in a region of space including $S$ , we have
$\displaystyle \int_C[A_1dx + A_2dy + A_3dz] =\\\vspace{0.2in} \underset{S}{\iint}\left[ \left( \frac{\partial A_3}{\partial y} -\frac{\partial A_2}{\partial z} \right)\cos\alpha + \left( \frac{\partial A_1}{\partial z} -\frac{\partial A_3}{\partial x} \right)\cos\beta + \left( \frac{\partial A_2}{\partial x} -\frac{\partial A_1}{\partial y} \right)\cos\gamma \right]dS \cdots(38)$
In vector form with $\bold{A} = A_1\bold{i} + A_2\bold{j} + A_3\bold{k}$ and $\bold{n} = \cos\alpha\bold{i} + \cos\beta\bold{j} + \cos\gamma\bold{k}$ , this is simply expressed as
$\displaystyle \int_C \bold{A}\cdot d\bold{r} = \underset{S}{\iint}(\nabla\times\bold{A})\cdot\bold{n}dS\cdots(39)$
In words this theorem, called Stoke’s theorem, states that the line integral of the tangential component of a vector $\bold{A}$ taken around a simple closed curve $C$ is equal to the surface integral of the normal component of the curl of $A$ taken over any surface $S$ having $C$ as a boundary. Note that if, as a special case $\nabla\times\bold{A} = 0$ in (39), we obtain the result (28).